电磁感应C

电磁感应C

编号：971205

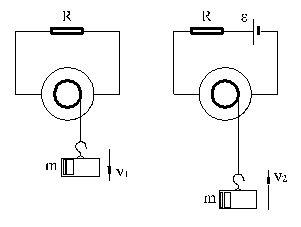15、如左图所示，有一内阻和损耗均不计的直流发电机，其定子的磁场恒定。先把它的转子线圈与一个电阻相连，再在电枢转轴上缠绕足够长的轻绳，绳下端悬挂一质量为m的重物，此重物最后会以v₁的速率匀速下落。现将一电动势为ε 、内阻不计的电源按右图接入电路，使发电机起电动机作用，则原重物最后会匀速上升，试求这个上升的速率v₂ 。

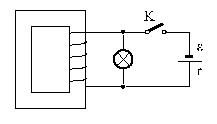16、右图中，灯泡电阻为15Ω，自感线圈的直流电阻为10Ω，电源电动势为4.0V、内阻为2.0Ω。试求：（1）K闭合稳定后，灯泡的电流；（2）K断开瞬间灯泡的电流方向及亮度变化情况。

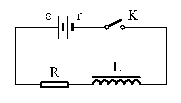
17、右图中，L = 0.4H ，R = 1.8Ω，电源电动势ε= 4.4V 、内阻r = 0.2Ω。当接通开关K时，电流强度在0.1s内平均变化0.5A 。试求这段时间内电流的平均值。

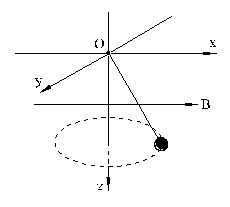18、图示为一个以O为原点的空间直角坐标系，z轴竖直向下，一根长50cm的质量不计的细金属丝上端悬于O点，下端吊小球P做圆锥摆运动。金属丝与z轴夹角37°，俯视逆时针旋转。若整个空间分布着+x方向的匀强磁场，且B = 0.2T ，重力加速度g取10m/s² 。试问：（1）P运动至何处时，金属丝两端电势相等？（2）P运动至何处时，P端电势比O端高？（3）电势差U_PO的最大值是多少？

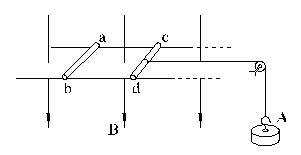19、如图所示，水平面内两平行金属导轨相距20cm ，其间有竖直方向的B = 0.5T的匀强磁场，导轨上置有两根导体金属棒ab和cd ，cd的中点被一与导轨平行的细线牵引，线的另一端绕过定滑轮悬挂砝码A ，已知质量m_ab = m_cd = m_A = 0.01kg ，棒的电阻R_ab = R_cd = 0.9Ω，导轨光滑、电阻不计。起初系统处于静止且绳子已被拉直。今将A释放，历时t = 6s后发现A的加速度达一稳定值，求6s末A的速度（重力加速度g取10m/s²）。

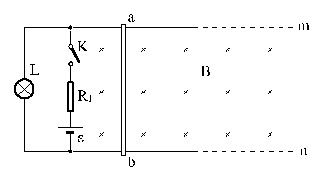
20、m、n为两根很长的、相距0.20m的水平金属导轨，且电阻不计。导轨左边接“6V，6W”的灯泡，电源电动势ε= 6.0V 、内阻不计，电阻R₁ = 1.0Ω。导轨中间放置电阻为2.0Ω的导体棒。B = 3.6T的匀强磁场充满整个导轨空间，方向如图。试求：（1）K合上瞬间，灯泡的功率；（2）灯泡最后的稳定功率和导体棒的最后稳定速度。

《电磁感应C》提示与答案

15、提示：能量关系 Gv₁ = R

　　　　　　　　　 I₂ε = R + Gv₂

　　　　  动力学关系 NBI₁S = M_G = NBI₂S

答案：ε－ v₁ 。

16、解略。

答案：（1）0.2A ；（2）向下，比原来更亮一下后“逐渐”熄灭。

17、说明：RL暂态函数 i =（1－），原则上可寻求题设过程在图象的哪一段，但中学途径不能求之精确解。

答案：约1.2A 。

18、提示：不计金属丝上的感应电流，锥摆会是匀速的。且 gtgθ= ω²lsinθ，解得ω= 5rad/s 。然后 U_m = BSω

答案：（1）yOz平面；（2）x ＞ 0 ；（3）0.06V 。

19、提示：设cd棒受安培力F（方向必向左），则 a_cd = a_A =  。要a_A定，F必定，即要求（v_cd － v_ab）定，可得 a_ab = a_cd = a_A =  。

同时解得 v_cd － v_ab = 6m/s

另据动量定理 mgt = 2mv_cd + mv_ab

答案：22m/s 。

20、提示：求ε_ab（稳定值）时，用戴维南定理更佳。

答案：（1）2.16W ；（2）4.41W ，7.14m/s 。