高三物理动量检测
一.选择题(每小题4分共48分)
1.下列运动过程中,在任意相等时间内,物体动量对时间的变化率相等的是
A.匀速圆周运动 B.自由落体运动 C.平抛运动 D.匀减速直线运动
2. 物块1、2的质量分别是m1=4kg和m2=1kg,它们具有的动能分别为E1和E2,且E1+E2=100J。若两物块沿同一直线相向运动发生碰撞,并粘在一起,欲使碰撞中损失的机械能最大,则E1和E2的值应该分别是
A.E1=E2=50J B.E1=20J,E2=80J C.E1=1J,E2=99J D.E1=90J,E2=10J
3. 一条捕鱼小船停靠在湖边码头,小船又窄又长(估计一吨左右)。一位同学想用一个卷尺粗略测定它的质量。他进行了如下操作:首先将船平行码头自由停泊,轻轻从船尾上船,走到船头后停下来,而后轻轻下船。用卷尺测出船后退的距离为d,然后用卷尺测出船长L,已知他自身的质量为m,则渔船的质量为
A.m(L+d)/d B.m(L-d)/d C.mL/d D.m(L+d)/d
![]() 4.如图所示,在一个足够大的光滑平面内有A、B两个质量相同的木块,中间用轻质弹簧相连 .今对B施以水平冲量F△t(△t极短).此后A、B的情况是
4.如图所示,在一个足够大的光滑平面内有A、B两个质量相同的木块,中间用轻质弹簧相连 .今对B施以水平冲量F△t(△t极短).此后A、B的情况是
(A)在任意时刻,A、B加速度大小相同 (B)弹簧伸长到最长时,A、B速度相同
(C)弹簧恢复到原长时,A、B动量相同 (D)弹簧压缩到最短时,系统总动能最小
5.汽车拉着拖车在平直的公路上匀速行驶,突然拖车与汽车脱钩,而汽车的牵引力不变,各自受的阻力不变,则在拖车停止运动前
(A)汽车和拖车的总动量不变 (B)汽车和拖车的总动能不变
(C)汽车和拖车的总动量增加 (D)汽车和拖车的总动能增加
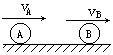 6、在光滑的水平面上,有A、B两个小球向右沿同一直线运动,取向右为正方向,两球的动量分别为pA=5kgm/s,pB=7kgm/s,如图所示。若两球发生正碰,则碰后两球的动量增量ΔpA、ΔpB可能是
6、在光滑的水平面上,有A、B两个小球向右沿同一直线运动,取向右为正方向,两球的动量分别为pA=5kgm/s,pB=7kgm/s,如图所示。若两球发生正碰,则碰后两球的动量增量ΔpA、ΔpB可能是
(A)ΔpA=3 kgm/s,ΔpB=3 kgm/s (B)ΔpA=-3 kgm/s,ΔpB=3 kgm/s
(C)ΔpA=3 kgm/s,ΔpB=-3 kgm/s (D)ΔpA=-10 kgm/s,ΔpB=10 kgm/s
7.向空中发射一物体,不计空气阻力,当此物体的速度恰好沿水平方向时,物体炸裂成a、b两块,若质量较大的a块的速度方向仍沿原来的方向,则
(A)b的速度方向一定与原来速度方向相同(B)在炸裂过程中,a、b受到的爆炸力的冲量一定相同(C)从炸裂到落地这段时间里,a飞行的水平距离一定比b的大
(D)a、b一定同时到达水平地面
8.甲、乙两物体的动量大小分别为P和P/2,动能大小分别为E和3E,那么
A.要使它们在相同时间内停下来,应对甲施加较大的阻力
B.要使它们在相同距离内停下来,应对乙施加较大的阻力
C.甲的质量是乙的12倍 D.乙的速度是甲的3倍
9. 在光滑水平面上,动能为E0,动量大小为p0的小钢球1与静止小钢球2发生碰撞,碰撞前后球1的运动方向相反.将碰撞后球1的动能和动量的大小分别计为E1、p1,球2的动能和动量的大小分别计为E2、p2,则必有
A.E1< E0 B.E2> E0 C.p1< p0 D.p2> p0
10. 在光滑水平地面上有两个相同的弹性小球A、B,质量都为m.现B球静止,A球向B球运动,发生正碰.已知碰撞过程中总机械能守恒,两球压缩最紧时的弹性势能为EP,则碰前A球的速度等于
A. ![]() B.
B. ![]() C. 2
C. 2![]() D. 2
D. 2![]()
 11. 竖直放置的轻弹簧,上端与质量为3kg的物块B相连接。另一个质量为1kg的物块A放在B上。先向下压A,然后释放,A、B共同向上运动一段路程后将分离。分离后A又上升了0.2m到达最高点,此时B的速度方向向下,且弹簧恰好为原长。则从A、B分离到A上升到最高点过程中,弹簧对B的冲量大小为(取g=10m/s2)
11. 竖直放置的轻弹簧,上端与质量为3kg的物块B相连接。另一个质量为1kg的物块A放在B上。先向下压A,然后释放,A、B共同向上运动一段路程后将分离。分离后A又上升了0.2m到达最高点,此时B的速度方向向下,且弹簧恰好为原长。则从A、B分离到A上升到最高点过程中,弹簧对B的冲量大小为(取g=10m/s2)
 A.1.2N s B.6.0N s
C.8.0N s D.12N s
A.1.2N s B.6.0N s
C.8.0N s D.12N s
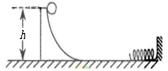
12. 如图所示,弹簧的一端固定在竖直墙上,质量为m的光滑弧形槽静止在光滑水平面上,底部与水平面平滑连接,一个质量也为m的小球从槽高h处开始下滑
A.在以后的运动过程中,小球和槽的动量始终守恒 B.在下滑过程中小球和槽之间的相互作用力始终不做功 C.桩弹簧反弹后,小球和槽都做速率不变的直线运动
D.被弹簧反弹后,小球和槽的机械能守恒,小球能回到槽高h处
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
 二.填空题(14分)
二.填空题(14分)
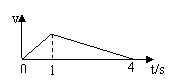
13.(4分)一物体在水平推力F作用下,由静止开始沿水平面运动,1s后撤去F,物体又继续向前滑行3s后停止.物体在运动过程受到的阻力为 .
14. 用半径相同的两小球A、B的碰撞验证动量守恒定律,实验装置示意如图,斜槽与水平槽圆滑连接。实验时先不放B球,使A球从斜槽上某一固定点 C由静止滚下,落到位于水平地面的记录纸上留下痕迹。再把B求静置于水平槽前端边缘处,让 A球仍从 C处由静止滚下,A球和 B球碰撞后分别落在记录纸上留下各自的痕迹。记录纸上的 O点是垂直所指的位置,若测得各落点痕迹到 O点的距离:OM=2.68cm,OP=8.62cm,ON=11.30cm,并知 A、B两球的质量比为 2:1,则未放 B球时 A球落地点是记录纸上的 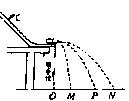 点。
点。
(1)入射小球1与被碰小球2应分别是 (2分)。(2)为了保证小球做平抛运动,必须调整斜槽使___________________(2分)。(3)继续实验步骤为:
A.在地面上依次铺白纸和复写纸。B.确定重锤对应点O。
C.不放球2,让球1从斜槽滑下,确定它落地点位置P。
D.把球2放在斜槽边缘,让球1从斜槽滑上,与球2正碰后,确定球1和球2落地点位置M和N。E.用刻度尺量OM、OP、ON的长度。F.看![]() 是否相等,以验证动量守恒。上述步骤有几步不完善或有错误,请指出并写出相应的正确步骤。(2分)
是否相等,以验证动量守恒。上述步骤有几步不完善或有错误,请指出并写出相应的正确步骤。(2分)
_______________________________________________________________________________
(4)(4分)系统碰撞前总动量 P与碰撞后总动量 P 的百分误差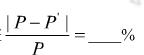
(结果保留二位有效数字)。
三.计算题(58分)
15.(12分)蹦床是运动员在一张绷紧的弹性网上蹦跳、翻滚并做各种空中动作的运动项目。一个质量为60kg的运动员,从离水平网面3.2m高处自由下落,着网后沿竖直方向蹦回到离水平网面5.0m高处.已知运动员与网接触的时间为1.2s.若把在这段时间内网对运动员的作用力当作恒力处理,求此力的大小.(g=10m/s2)
16.(14分)如图所示,水平光滑地面上停放着一辆小车,左侧靠在竖直墙壁上,小车的四分之一圆弧轨道AB是光滑的,在最低点B与水平轨道BC相切,BC的长度是圆弧半径的10倍,整个轨道处于同一竖直平面内。可视为质点的物块从A点正上方某处无初速下落,恰好落入小车圆弧轨道滑动,然后沿水平轨道滑行至轨道末端C处恰好没有滑出。已知物块到达圆弧轨道最低点B时对轨道的压力是物块重力的9倍,小车的质量是物块的3倍,不考虑空气阻力和物块落入圆弧轨道时的能量损失(g=10m/s2)。求:
(1)物块开始下落的位置距水平轨道BC的竖直高度是圆弧半径的几倍;
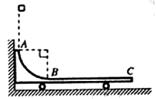 (2)物块与水平轨道BC间的动摩擦因数μ。
(2)物块与水平轨道BC间的动摩擦因数μ。
17.(16分)如图14所示,在同一竖直上,质量为2m的小球A静止在光滑斜面的底部,斜面高度为H=2L。小球受到弹簧的弹性力作用后,沿斜面向上运动。离开斜面后,达到最高点时与静止悬挂在此处的小球B发生弹性碰撞,碰撞后球B刚好能摆到与悬点O同一高度,球A沿水平方向抛射落在水平面C上的P点,O点的投影O'与P的距离为L/2。已知球B质量为m,悬绳长L,视两球为质点,重力加速度为g,不计空气阻力,求:
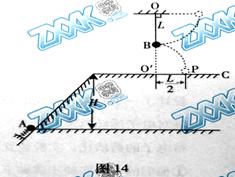 (1)球B在两球碰撞后一瞬间的速度大小;
(1)球B在两球碰撞后一瞬间的速度大小;
(2)球A在两球碰撞后一瞬间的速度大小;
(3)弹簧的弹性力对球A所做的功。
18. (16分)如图所示,一质量M=2kg的长木板B静止于光滑水平面上,B的右边放有竖直挡板.现有一小物体A(可视为质点)质量m=1kg,以速度v0=6m/s从B的左端水平滑上B,已知A和B间的动摩擦因数μ=0.2,B与竖直挡板的碰撞时间极短,且碰撞时无机械能损失(g=10m/s2).
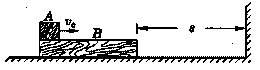 (1)若B的右端距挡板s=4m,要使A最终不脱离B,则木板B的长度至少多长?
(1)若B的右端距挡板s=4m,要使A最终不脱离B,则木板B的长度至少多长?
(2)若B的右端距挡板s=0.5m,要使A最终不脱离B,则木板B的长度至少多长?
19(选做题)在光滑的水平面上沿直线按不同的间距依次排列着质量均为m的滑块,1、2、3、…(n-1)、n,滑块P的质量也为m.P从静止开始在大小为F的水平恒力作用下向右运动,经时间T与滑块1碰撞,碰撞后滑块便粘连在一起.以后每经过时间T就与下一滑块碰撞一次,每次碰撞后均粘连在一起,每次碰撞时间极短,每个物块都可简化为质点.求:
第n-1个滑块与第n个滑块间的距离sn-1.
参考答案
1 BCD2 B3 B 4、ABD5、AD 6、B 7、D8、ABC9. ACD10. C11 B.12. C
11、f=F/4 14. (1)AB(2)其末端切线水平 (3)D选项中,球1应从与C项相同高度滑下;P、M、N点应该是多次实验落地点的平均位置。(4) 3.4
15. F=1.5×103N 16. (1)设物块的质量为m,其开始下落处的位置距BC的竖直高度为h,到达B点时的速度为v,小车圆弧轨道半径为R。由机械能守恒定律,有:mgh=mv2
根据牛顿第二定律,有:9mg-mg=m解得h=4R
则物块开始下落的位置距水平轨道BC的竖直高度是圆弧半径的4倍。
(2)设物块与BC间的滑动摩擦力的大小为F,物块滑到C点时与小车的共同速度为v',物块在小车上由B运动到C的过程中小车对地面的位移大小为s。依题意,小车的质量为3m,BC长度为10R。由滑动摩擦定律有: F=μmg
由动量守恒定律,有mv=(m+3m)v' 对物块、小车分别应用动能定理,有
-F(10R+s)=mv'2 -mv2 Fs=(3m)v'2-0 μ=0.3
17.. (1)设碰撞后的一瞬间,球B的速度为vB/,由于球B恰好与悬点O同一高度,根据动能定理:
![]() ①
① ![]() ②
②
(2)球A达到最高点时,只有水平方向速度,与球B发生弹性碰撞.设碰撞前的一瞬间,球A水平方向速度为vx.碰撞后的一瞬间,球A速度为vx/.球A、B系统碰撞过程中动量守恒和机械能守恒: ![]() ③
③ ![]() ④
④
由②③④解得:![]() ⑤
⑤
及球A在碰撞前的一瞬间的速度大小![]() ⑥
⑥
(3)碰后球A作平抛运动.设从抛出到落地时间为t,平抛高度为y,则:![]() ⑦
⑦
![]() ⑧
⑧
由⑤⑦⑧得:y=L
以球A为研究对象,弹簧的弹性力所做的功为W,从静止位置运动到最高点:
![]() ⑨
⑨
由⑤⑥⑦得:W=![]() mgL
⑩
mgL
⑩
18. (1)碰一次8.7m(2)碰二次8.96m
19、解析:
因每次碰撞时间极短,对从开始到发生第n次碰撞后瞬间应用动量定理,有
FnT=(n+1)mvn ⑥
解得vn=![]() ⑦
⑦
(3)同理可以求出第(n-1)次碰后的速度vn-1=![]() ⑧
⑧
对第n次碰撞前全过程应用动量定理
FnT=nmun ⑨
解得un=![]() ⑩(与n无关)
⑩(与n无关)
对n-1到n之间应用动能定理,有
Fsn-1=![]()
解得sn-1=![]()