高三物理机械能检测题2-高中三年级物理试题练习、期中期末试卷、测验题、复习资料-高中物理试卷-试卷下载

高三物理机械能检测题2

一.选择题(每空4分，共48分)

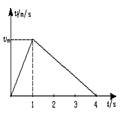
1. 在平直公路上，汽车由静止开始做匀加速运动，当速度达到v_m后立即关闭发动机直到停止，v－t图象如图所示.设汽车的牵引力为F，摩擦力为F_f,全过程中牵引力做功W₁，克服摩擦力做功W₂，则

A.F∶F_f=1∶3　　　　B.F∶F_f=4∶1C.W₁∶W₂=1∶1 .DW₁∶W₂=1∶3

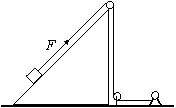2. 如图，卷扬机的绳索通过定滑轮用力F 拉位于粗糙斜面上的木箱，使之沿斜面加速向上移动。在移动过程中，下列说法正确的是

A．F对木箱做的功等于木箱增加的动能与木箱克服摩擦力

所做的功之和B．F对木箱做的功等于木箱克服摩擦力和克服重力所做的功之和C．木箱克服重力做的功等于木箱增加的重力势能D．F对木箱做的功等于木箱增加的机械能与木箱克服摩擦力做的功之和

3. 在光滑水平面上有a、b两质点，其质量均为2.0kg，a质点只在水平恒力F_a=4.0N作用下由静止开始运动了4.0s，b质点只在水平恒力F_b=16N作用下由静止开始移动了4.0m。比较这两个过程，可以得出的正确结论是　　

A.a质点获得的动量比b质点的大　　　　B.a质点获得的动能比b质点的少

C.力F_a做的功比力F_b做的功多　　　　 D.以上三种说法都不对

4. 质量为m的木块静止在光滑水平面上，受到水平恒力F的作用，经过时间t，木块的位移为s，则在时刻t，外力的瞬时功率为　

A.　　B.　　C.　　D.

5. 如图所示，一个质量为m的物体以某一速度从A点冲上倾角为30°的斜面，其运动的加速度为3g/4，这物体在斜面上上升的最大高度为h，则在上升过程中物体：

　 A、重力势能增加了;　 B、机械能损失了;

　 C、动能损失了mgh ;　 D、重力势能增加了mgh

6. 假定地球，月球都静止不动，用火箭从地球沿地月连线向月球发射一探测器。假定探测器在地球表面附近脱离火箭。用W表示探测器从脱离火箭处飞到月球的过程中克服地球引力做的功，用E_k表示探测器脱离火箭时的动能，若不计空气阻力，则

A．E_k必须大于或等于W，探测器才能到达月球　B．E_k小于W，探测器也可能到达月球　

C．E_k＝W，探测器一定能到达月球　D．E_k＝W，探测器一定不能到达月球

7. 物体以100J的初动能从斜面底端向上滑行，第一次将过P点时间，它的动能比最初减少60J，势能比最初增大了45J，则物体从斜面顶端返回底端时，其末动能应等于

A、60J 　 B、50J 　　　　C、48J 　　　　 D、20J

8. 我国绕月探测工程的预先研究和工程实施已取得重要进展。设地球、月球的质量分别为m₁、m₂，半径分别为R₁、R₂，人造地球卫星的第一宇宙速度为ｖ，对应的环绕周期为Ｔ，则环绕月球表面附近圆轨道飞行的探测器的速度和周期分别为

Ａ．v，T　Ｂ．v，T

Ｃ．v，T　Ｄ． v，T

9. 一个小球从固定在地面的竖直轻弹簧的正上方的高处自由落下，小球在运动过程中受到的空气阻力忽略不计。则在小球从接触弹簧开始到将弹簧压缩到最短的运动过程中，以下关于能量或动量关系的说法正确的是　　

A．小球受到的合外力对小球做的功等于小球动能的变化

B．弹性势能和重力势能总和先增大后减小 C．弹性势能和重力势能总和先减小后增大

D．小球受到的合外力的冲量等于小球动量的变化

10. 美国的NBA篮球赛非常精彩，吸引了众多观众.经常有这样的场面：在临终场0.1s的时候，运动员把球投出且准确命中，获得比赛的胜利.如果运动员投篮过程中对篮球做功为W，出手高度为h₁，篮筐距地面高度为h₂，球的质量为，空气阻力不计，则篮球进筐时的动能为

A．W+ B．W+ C．－W　D．－W

11. 质量相同的三个小球，从同一高度处以相同的速率分别沿水平方向、竖直向上和竖直向下三个方向抛出。若不计空气阻力，则三个小球落地时具有相同的：

　 A、速度　　　　B、速率　　　　C、动量　　　　D、动能

12. 一木块静止在光滑的水平面上，被水平飞来的子弹击中且未穿出，在此过程中子弹所受的阻力的反作用力就是使木块向前运动的动力。则下列说法正确的是：

A、在此过程中，木块和子弹的内能都增加； B、子弹损失的机械能等于木块增加的机械能； C、阻力对子弹所做的功大小等于动力对木块所做的功；

D、子弹和木块组成的系统的总能量保持不变。

题号	1	2	3	4	5	6	7	8	9	10	11	12
答案

二.填空题（共18分）

13. （4分）人的心脏每跳一次大约输送8×10^-5 m³的血液，正常人血压（可看做心脏输送血液的压强）的平均值为1.5×10⁴ Pa,心跳约每分钟70次.据此估测心脏工作的平均功率约为_____W.

14. 用落体验证机械能守恒定律的实验

（1）（4分）为进行该实验，备有下列器材可供选择

铁架台、打点计时器、复写纸片、纸带、低压直流电源、天平、秒表、导线、开关。　　其中不必要的器材是　　　　　　　　　　　。缺少的器材是　　　　　　　　　　　。

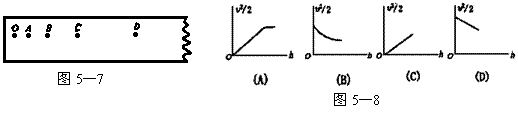
（2）（6分）若实验中所用重物的质量m=1㎏，打点时间间隔为0.02s，打出的纸带如图5—7所示，O、A、B、C、D为相邻的几点，测的OA=0.18cm、OB=0.76㎝、OC=1.71㎝、OD=3.04㎝，查出当地的重力加速度g=9.80，则重物在B点时的动能E_AB=　　　　 J。从开始下落到B点的过程中，重物的重力势能减少量是　　　　　　 J，由此得出的结论是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　。(计算结果保留三位有效数字)

（3）（4分）根据纸带算出相关各点的速度v量出下落的距离h，以为纵轴，以h为横轴画出的图线应是图5—8中的　　　　　，就证明机械能是守恒的，图像的斜率代表的物理量是　　　　　　　　。

三.计算题（共56分）

15. （11分）电动机通过一绳子吊起质量为8 kg的物体，绳的拉力不能超过120 N，电动机的功率不能超过1200 W，要将此物体由静止起用最快的方式吊高90 m（已知此物体在被吊高接近90 m时已开始以最大速度匀速上升），所需时间为多少？

16.（11分）倾斜雪道的长为25 m，顶端高为15 m，下端经过一小段圆弧过渡后与很长的水平雪道相接，如图所示。一滑雪运动员在倾斜雪道的顶端以水平速度v₀＝8 m/s飞出，在落到倾斜雪道上时，运动员靠改变姿势进行缓冲使自己只保留沿斜面的分速度而不弹起。除缓冲外运动员可视为质点，过渡轨道光滑，其长度可忽略。设滑雪板与雪道的动摩擦因数μ＝0.2，求运动员在水平雪道上滑行的距离（取g＝10 m/s2）

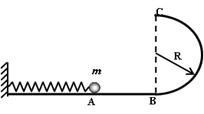17.（12分）如图所示，光滑水平面AB与竖直面内的半圆形导轨在B点衔接，导轨半径为R，一个质量为m的静止的小球在A处压缩弹簧，释放小球后，在弹簧弹力的作用下小球获得一向右的速度，当它经过B点进入导轨瞬间对导轨的压力为其重力的7倍，之后向上运动恰好能沿轨道运动到C点，求：

⑴释放小球前弹簧的弹性势能

⑵小球由B到C克服阻力做的功

⑶物体离开C点后落回水平面时的动能的大小

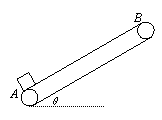18.（12分）如图所示，传送带与水平面夹角为θ=30°，其上、下两端点A、B间的距离是5.0m。传送带在电动机的带动下，以1.0m/s顺时针匀速运转。现将一质量为10kg的物体（可视为质点）轻放于传送带的A点，已知物体与传送带间的动摩擦因数为/2，则在传送带将物体从A点传送到B点过程中，求：

⑴传送带对物体做了多少功？

⑵为传送该物体，电动机额外需要做多少功？

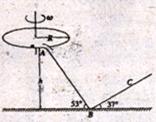
19.（10分）如图所示，一水平圆盘绕过圆心的竖直轴转动，圆盘边缘有一质量m=1.0kg的小滑块。当圆盘转动的角速度达到某一数值时，滑块从圆盘边缘滑落，经光滑的过渡圆管进入轨道ABC。以知AB段斜面倾角为53°，BC段斜面倾角为37°，滑块与圆盘及斜面间的动摩擦因数均μ=0.5　，A点离B点所在水平面的高度h=1.2m。滑块在运动过程中始终未脱离轨道，不计在过渡圆管处和B点的机械能损失，最大静摩擦力近似等于滑动摩擦力，取g=10m/s²,sin37°=0.6; cos37°=0.8

（1）若圆盘半径R=0.2m，当圆盘的角速度多大时，滑块从圆盘上滑落？

（2）若取圆盘所在平面为零势能面，求滑块到达B点时的机械能。

（3）从滑块到达B点时起，经0.6s 正好通过C点，求BC之间的距离。