高三物理动量专题练习2

高三物理动量专题练习2

1.如图所示，A、B两滑块的质量均为m，分别穿在光滑的足够长的水平固定导杆上，两导杆平行，间距为d。用自然长度也为d的轻弹簧连接两滑块。开始时两滑块均处于静止状态，今给滑块B一个向右的瞬时冲量I，求以后滑块A的最大速度。

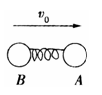2.某宇航员在太空站内做了如下实验：选取两个质量分别为m_A=0.1kg、m_B=0.2kg的小球A、B和一根轻质短弹簧，弹簧的一端与小球A粘连，另一端与小球B接触而不粘连．现使小球A和B之间夹着被压缩的轻质弹簧，处于锁定状态，一起以速度v₀=0.1m/s做匀速直线运动，如图所示．过一段时间，突然解除锁定（解除锁定没有机械能损失），两球仍沿原直线运动，从弹簧与小球B刚刚分离开始计时，经时间t=3.0s，两球之间的距离增加了s=2.7m，求弹簧被锁定时的弹性势能E_p?

3.如图所示，光滑轨道的DP段为水平轨道，PQ段为半径是R的竖直半圆轨道，半圆轨道的下端与水平的轨道的右端相切于P点．一轻质弹簧两端分别固定质量为2m的小球A和质量为m的小球B，质量为m小球C靠在B球的右侧．现用外力作用在A和C上，弹簧被压缩（弹簧仍在弹性限度内）．这时三个小球均静止于距离P端足够远的水平轨道上．若撤去外力，C球恰好可运动到轨道的最高点Q．已知重力加速度为g．求撤去外力前的瞬间，弹簧的弹性势能E是多少？

4.如图所示，两个质量均为4m的小球A和B由轻弹簧连接，置于光滑水平面上．一颗质量为m子弹，以水平速度v₀射入A球，并在极短时间内嵌在其中．求：在运动过程中

（1）什么时候弹簧的弹性势能最大，最大值是多少？

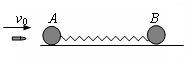（2）A球的最小速度和B球的最大速度．

5.如图所示，A、B两个矩形木块用轻弹簧相接静止在水平地面上，弹簧的劲度系数为k，木块A和木块B的质量均为m．若弹簧的劲度系数k是未知的，将一物体C从A的正上方某位置处无初速释放，C与A相碰后立即粘在一起（不再分离）向下运动，它们到达最低点后又向上运动．已知C的质量为m时，把它从距A高为H处释放，则最终能使B刚好离开地面．若C的质量为，要使B始终不离开地面，则释放时，C距A的高度h不能超过多少？

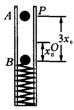6.质量为m的小球B用一根轻质弹簧连接．现把它们放置在竖直固定的内壁光滑的直圆筒内，平衡时弹簧的压缩量为x₀，如图所示，小球A从小球B的正上方距离为3 x₀的P处自由落下，落在小球B上立刻与小球B粘在一起向下运动，它们到达最低点后又向上运动，并恰能回到O点（设两个小球直径相等，且远小于x₀，略小于直圆筒内径），已知弹簧的弹性势能为，其中k为弹簧的劲度系数，为弹簧的形变量．求：

(1）小球A的质量．(2）小球A与小球B一起向下运动时速度的最大值．

参考答案

1. 弹簧恢复原长时A的速度达最大，设为，设此时B的速度为。由系统动量守恒和机械能守恒定律得

经求解可知　　　　

2. 取A、B为系统，由动量守恒得　①

又根据题意得：　②由①②两式联立得：v_A=0.7m/s，v_B =－0.2m/s

由机械能守恒得：　 ③代入数据解得E_p=0.027J

3. 解析：对A、B、C及弹簧组成的系统，当弹簧第一次恢复原长时，设B、C共同速度大小为v₀，A的速度大小为v_A，由动量守恒定律有

①则v_A=v₀由系统能量守恒有E=2mv_A²＋(m＋m)v₀² ②

此后B、C分离，设C恰好运动至最高点Q的速度为v,此过程C球机械能守恒，则

mg·2R=mv₀²－mv²③在最高点Q，由牛顿第二定律得　　　 ④

联立①～④式解得E=10mgR

4. 解析：子弹与A球发生完全非弹性碰撞，子弹质量为m，A球、B球分别都为M，子弹与A球组成的系统动量守恒，则

mv₀= (m+M)V　　　　　　　①

（1）以子弹、A球、B球作为一系统，以子弹和A球有共同速度为初态，子弹、A球、B球速度相同时为末态，则

（m+M）V= (m+M+M)V′　 ②　　③

M＝4m，解得　　④

（2）以子弹和A球有共同速度为初态，子弹和A球速度最小、B球速度最大为末态，则（m+M）V= (m+M)V_A+MV_B　　 ⑤　⑥

解得，_⑦或＝v0，＝0　　　　　　 ⑧

根据题意求A球的最小速度和B球的最大速度，所以V_Amin，V_Bmax

5. 解析：

物块C的质量为m时，它自由下落H高度时的速度　　①

设C与A碰撞后的共同速度为v₂，根据动量守恒定律，有

则　　　　　　　　　　 ②

以后A、C继续压缩弹簧，后又向上弹起，最终能使木块B刚好离开地面．此过程中，A、C上升的高度为上升的高度为，由于最初弹簧的压缩量x₁与最后的伸长量x₂相等，所以，弹簧势能相等，根据机械能守恒定律，有

　　　　③

物块C的质量为时，设在距A高h处自由下落后刚好能使木块B离开地面．

则C下落h高度时的速度　 ④设C与A碰撞后的共同速度为．则有解得 ⑤

A、C碰后上升高度时，木块B刚好离开地面，此过程中，由机械能守恒定律有

⑥由以上各式消去解得

6. 解：(1）由平衡条件得mg = k x₀，设球A的质量为m，与球B碰撞前的速度为v₁，由机械能守恒定律得设球A、B结合后的速度为，由动量守恒定律得

由于球A、B恰能回到O点，根据动能定理得

解之得 .

(2）由B点向下运动的距离为x₁时速度最大，加速度为零．即，因为，，所以．由机械能守恒得

.