高三物理复习动量综合测试（A卷）
第一部分 选择题（共40分）
一.本题共10小题，每小题4分，共40分.在每小题给出的四个选项中，有的小题只有一个选项正确，有的小题有多个选项正确。全部选对的得4分，选对但不全的得2分，有选错的或不答的得0分．
１.质量为2kg的小车以2m/s的速度沿光滑的水平面向右运动，若将质量为2kg的砂袋以3m/s的速度迎面扔上小车，则砂袋与小车一起运动的速度的大小和方向是
A．2.6m/s，向右 B．2.6m/s，向左 C．0.5m/s，向左 D．0.8m/s，向右
2.在光滑水平面上，两球沿球心连线以相等速率相向而行，并发生碰撞，下列现象可能的是
A．若两球质量相同，碰后以某一相等速率互相分开
B．若两球质量相同，碰后以某一相等速率同向而行
C．若两球质量不同，碰后以某一相等速率互相分开
D．若两球质量不同，碰后以某一相等速率同向而行
3.在空间某一点以大小相等的速度分别竖直上抛、竖直下抛、水平抛出质量相等的小球，不计空气阻力，经过t秒（设小球均未落地）
A．做上抛运动的小球动量变化最大
B．三个小球动量变化大小相等
C．做平抛运动的小球动量变化最小
D．三个小球动量变化相等
4.如图所示,a、b、c三个相同的小球,a从光滑斜面顶端由静止开始自由下滑,同时b、c从同一高度分别开始自由下落和平抛.下列说法正确的有
A.它们同时到达同一水平面
B.重力对它们的冲量相同
C.它们的末动能相同
D.它们动量变化的大小相同
5. 向空中发射一物体，不计空气阻力，当此物体的速度恰好沿水平方向时，物体炸裂成a、b两块，若质量较大的a块的速度方向仍沿原来的方向，则
A.b的速度方向一定与原来速度方向相同
B.在炸裂过程中，a、b受到的爆炸力的冲量一定相同
C.从炸裂到落地这段时间里，a飞行的水平距离一定比b的大
D.a、b一定同时到达水平地面
6.如图所示，A、B两物体的质量比mA∶mB=3∶2，它们原来静止在平板车C上，A、B间有一根被压缩了的弹簧，A、B与长平板车的上表面间动摩擦因数相同，地面光滑.当弹簧突然释放后，则有
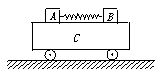
A.A、B系统动量守恒 B.A、B、C系统动量守恒
C.小车向左运动 D.小车向右运动
7.如图所示,一根轻弹簧下端固定,竖立在水平面上.其正上方A位置有一只小球.小球从静止开始下落,在B位置接触弹簧的上端,在C位置小球所受弹力大小等于重力,在D位置小球速度减小到零,小球下降阶段下列说法中正确的是
A.在B位置小球动能最大
B.在C位置小球动能最大
C.从A→C位置小球重力势能的减少大于小球动能的增加
D.从A→D位置小球重力势能的减少等于弹簧弹性势能的增加
8.如图所示，两带电金属球在绝缘的光滑水平桌面上沿同一直线相向运动，A球带电为-q，B球带电为+2q，下列说法中正确的是
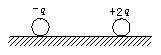
A.相碰前两球的运动过程中，两球的总动量守恒
B.相碰前两球的总动量随两球的距离逐渐减小而增大
C.相碰分离后的两球的总动量不等于相碰前两球的总动量，因为两球相碰前作用力为引力，而相碰后的作用力为斥力
D.相碰分离后任一瞬时两球的总动量等于碰前两球的总动量，因为两球组成的系统合外力为零
9.如图所示的装置中,木块B与水平桌面间的接触是光滑的,子弹A沿水平方向射入木块后留在木块内,将弹簧压缩到最短.将子弹、木块和弹簧合在一起作为研究对象(系统),则此系统从子弹开始射入木块到弹簧压缩到最短的整个过程中
A.动量守恒,机械能守恒
B.动量不守恒,机械能不守恒
C.动量守恒,机械能不守恒
D.动量不守恒,机械能守恒
10.如图所示，质量为m的子弹以速度υ0水平击穿放在光滑水平地面上的木块。木块长为L，质量为M，木块对子弹的阻力恒定不变，子弹穿过木块后木块获得动能为Ek，若仅木块或子弹的质量发生变化，但子弹仍能穿过木块，则
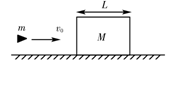A．M不变，m变小，则木块获得的动能一定变大
B．M不变，m变小，则木块获得的动能可能变大
C．m不变，M变小，则木块获得的动能一定变大
D．m不变，M变小，则木块获得的动能可能变大
第二部分 非选择题（共110分）
二.本题共8小题，共110分.按题目要求作答．解答题应写出必要的文字说明、方程式和
重要演算步骤．只写出最后答案的不能得分．有数值计算的题，答案中必须明确写出数
值和单位．
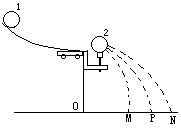
11．（10分）图为“碰撞中的动量守恒”实验装置示意图。
（1）入射小球1与被碰小球2直径相同，均为d，它们的质量相比较，应是m1____m2.
（2）为了保证小球做平抛运动，必须调整斜槽使________________________。
（3）继续实验步骤为：
A．在地面上依次铺白纸和复写纸。
B．确定重锤对应点O。
C．不放球2，让球1从斜槽滑下，确定它落地点位置P。
D．把球2放在立柱上，让球1从斜槽滑下，与球2正碰后，确定球1和球2落地点位置M和N。
E．用刻度尺量出OM、OP、ON的长度。
F．看
是否相等，以验证动量守恒。
上述步骤有几步不完善或有错误，请指出并写出相应的正确步骤。
_____________________________________________________________________________
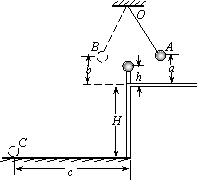12.（10分）右图是用来验证动量守恒的实验装置，弹性球1用细线悬挂于O点，O点下方桌子的边沿有一竖直立柱．实验时，将球1拉到A点，并使之静止，同时把球2放在立柱上．释放球1，当它摆到悬点正下方时与球2发生对心碰撞．碰后球1向左最远可摆到B点，球2落到水平地面上的C点．测出有关数据即可验证1、2两球碰撞时动量守恒．现已测出A点离水平桌面的距离为a．B点离水平桌面的距离为b，C点与桌子边沿间的水平距离为c．此外，还需要测量的量是_________、________________、和_____________________．根据测量的数据，该实验中动量守恒的表达式为__________________________．
13.（13分）如图所示，光滑水平面上静止放着长L=1.6m，质量为M=3kg的木块（厚度不计），一个质量为m=1kg的小物体放在木板的最右端，m和M之间的动摩擦因数μ=0.1，今对木板施加一水平向右的拉力F，（g取10m/s2）
(1)为使小物体不掉下去，F不能超过多少？
(2)如果拉力F=10N恒定不变，求小物体所能获得的最大动能？
(3)如果拉力F=10N，要使小物体从木板上掉下去，拉力F作用的时间至少为多少？
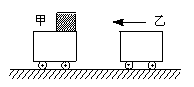
14.（13分）如图所示，甲车质量为
，静止在光滑水平面上，上表面光滑，右端放一个质量为
的小物体. 乙车质量为
，以
的速度向左运动，与甲车碰撞后，甲车获得
的速度，物体滑到乙车上. 若乙车足够长，上表面与物体的动摩擦因数为
，求：
（1）甲、乙两车碰后瞬间，乙车的速度；
（2）物体在乙车表面上滑行多长时间相对乙车静止？（取
）
15.（15分）设质量为m的子弹以初速度v0射向静止在光滑水平面上的质量为M的木块，并留在木块中不再射出，子弹钻入木块深度为d。求木块对子弹的平均阻力的大小和该过程中木块前进的距离。
16.（15分）如图所示，光滑水平面上，质量为2m的小球B连接着轻质弹簧，处于静止；质量为m的小球A以初速度v0向右匀速运动，接着逐渐压缩弹簧并使B运动，过一段时间，A与弹簧分离，设小球A、B与弹簧相互作用过程中无机械能损失，弹簧始终处于弹性限度以内
（1）求当弹簧被压缩到最短时，弹簧的弹性势能E．
（2）若开始时在小球B的右侧某位置固定一块挡板(图中未画出)，在小球A与弹簧分离前使小球B与挡板发生正撞，并在碰后立刻将挡板撤走．设小球B与固定挡板的碰撞时间极短，碰后小球B的速度大小不变、但方向相反。设此后弹簧弹性势能的最大值为
，试求可能值的范围．
17.（17分）质量为M的小车A左端固定一根轻弹簧，车静止在光滑水平面上，一质量为m的小物块B从右端以速度v0冲上小车并压缩弹簧，然后又被弹回，回到车的右端时刚好与车保持相对静止.
（1）求这过程弹簧的最大弹性势能EP和全过程系统摩擦生热Q各为多少？
（2）简述B相对于车向右返回过程中小车的速度变化情况.
A B
18.（17分）如图所示，光滑的水平轨道接一个半径为R的光滑半圆轨道，在水平轨道上有2002个质量相同的小球.除第1号小球外，其他小球均静止.第1号小球以初速度v0碰撞第2号小球，在碰撞过程中损失初动能的
；第2号小球碰撞第3号小球，在碰撞过程中损失第2号小球初动能的；第3号小球又碰撞第4号小球，依次碰撞下去，每次碰撞均损失前一小球初动能的，最后，第2002号小球恰能沿半圆轨道达到最高点.试求第1号小球的初速度v0.
动量综合测试（B卷）
第一部分 选择题（共40分）
一.本题共10小题，每小题4分，共40分.在每小题给出的四个选项中，有的小题只
有一个选项正确，有的小题有多个选项正确。全部选对的得4分，选对但不全的得
2分，有选错的或不答的得0分．
1．关于冲量，以下说法正确的是
A.只要物体受到力的作用，物体受到的总冲量就一定不为零
B.只要物体受到的合外力不为零，物体在任一Δt时间内所受的总冲量就一定不为零
C.如果力是恒力，则冲量的方向就是该力的方向
D.做曲线运动的物体，在任何Δt时间内所受的总冲量一定不为零
2．1924年法国物理学家德布罗意提出物质波的概念：任何一个运动着的物体，小到电子，大到行星、恒星都有一种波与之对应，波长为λ = 
，P为物体运动的动量，h是普朗克常量．同样光也具有粒子性，光子的动量为：P = 
．根据上述观点可以证明一个静止的自由电子如果完全吸收一个γ光子，会发生下列情况：设光子频率为ν，则E = hν，P = = 
，被电子吸收后有hν = 
meυ2，h
= meυ，解得：υ = 2C．电子的速度为光速的2倍，显然这是不可能的。关于上述过程以下说法正确的是
A．因为在微观世界动量守恒定律不适用，上述论证错误，电子有可能完全吸收一个电子
B．因为在微观世界能量守恒定律不适用，上述论证错误，电子有可能完全吸收一个电子
C．动量守恒定律，能量守恒定律是自然界中普遍适用的规律，所以唯一结论是电子不可能完全吸收一个r光子
D．若γ光子与一个静止的自由电子发生作用，则r光子被电子散射后频率会减小
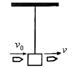
3．如图所示，用细线挂一质量为M的木块，有一质量为m的子弹自左向右水平射穿此木块，穿透前后子弹的速度分别为v０和v（设子弹穿过木块的时间和空气阻力不计），木块的速度大小为
A．
B．
C．
D．
4．放在光滑水平面上的A、B两小车中间夹了一压缩轻质弹簧，用两手分别控制小车处于静止状态，下面说法中正确的是
A．两手同时放开后，两车的总动量为零
B．先放开右手，后放开左手，两车的总动量向右
C．先放开左手，后放开右手，两车的总动量向右
D．两手同时放开，两车总动量守恒；两手放开有先后，两车总动量不守恒
5．一个电子(质量为m、电荷量为-e)和一个正电子(质量为m、电荷量为e)经电场加速后以相等的动能Ek相向运动，并撞到一起，发生“湮灭”，产生两个频率相同的光子.设产生光子的频率为v，若这两个光子的能量都是hv，动量分别为p和p＇，下列关系式中正确的是
A. hv=mc2，p=p＇
B. hv=
mc2，p=p＇
C. hv=mc2+Ek，p= -p＇
D. hv=(mc2+Ek)，p= -p＇
6．在质量为M的小车中挂有一单摆，摆球的质量为 m
，小车和单摆以恒定的速度V沿光滑水平地面运动，与位于正对面的质量为m的静止木块发生碰撞，碰撞的时间极短，在此碰撞过程中，下列说法可能发生的是：
Ａ.小车、木块、摆球的速度都发生变化，分别变为V
、V
、V
，满足
(M+ m)V=M V+ m V+ m V
Ｂ.摆球的速度不变，小车和木块的速度变为V和V，满足MV=M V+ m V
Ｃ.摆球的速度不变，小车和木块的速度都变为V，满足MV=（M+ m）V
Ｄ.小车和摆球的速度都变为V，木块的速度变为V，满足
（M+ m）V=（M+ m）V+ m V
7.两个小球在光滑水平面上沿同一直线，同一方向运动，B球在前，A球在后，MA=1kg, MB=2kg, vA=6m/s, vB=2m/s, 当A球与B球发生碰撞后，A、B两球速度可能为
A. vA=5m/s, vB=2.5m/s B. vA=2m/s, vB=4m/s
C . vA= -4m/s, vB=7m/s D. vA=7m/s, vB=1.5m/s
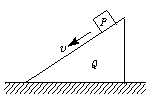
8.将物体P从置于光滑水平面上的斜面体Q的顶端以一定的初速度沿斜面往下滑，如图所示.在下滑过程中，P的速度越来越小，最后相对斜面静止，那么由P和Q组成的系统
A. 动量守恒
B. 水平方向动量守恒
C. 最后P和Q以一定的速度共同向左运动
D. 最后P和Q以一定的速度共同向右运动
9.长木板A放在光滑的水平面上,质量为m=2kg的另一物体B以水平速度v0=2m/s滑上原来静止的长木板A的表面,由于A、B间存在摩擦,之后A、B速度随时间变化情况如图所示,则下列说法正确的是
A.木板获得的动能为1J
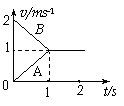
B.系统损失的机械能为2J
C.木板A的最小长度为1m
D. A、B间的动摩擦因数为0.1
10.A、B两滑块在一水平长直气垫导轨上相碰.用频闪照相机在t0=0,
t1=Δt,t2=2Δt, t3=3Δt各时刻闪光四次,摄得如图所示照片,其中B像有重叠,mB=
mA,由此可判断
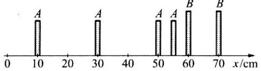A. 碰前B静止,碰撞发生在60cm处, t=2.5Δt时刻
B. 碰后B静止,碰撞发生在60cm处, t=0.5Δt时刻
C. 碰前B静止,碰撞发生在60cm处, t=0.5Δt时刻
D. 碰后B静止,碰撞发生在60cm处, t=2.5Δt时刻
第二部分 非选择题（共110分）
二.本题共8小题，共110分.按题目要求作答．解答题应写出必要的文字说明、方程式和
重要演算步骤．只写出最后答案的不能得分．有数值计算的题，答案中必须明确写出数
值和单位．
11.（8分）如图1所示装置验证碰撞中的动量守恒，A、B两球直径相同，质量分别为m1、m2.
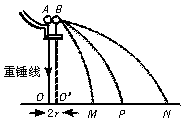
图1
（1）实验中所必须用的测量工具是_______、_______.
（2）某次实验得出小球的落点情况如图2所示，若碰撞中动量守恒，则两小球质量之比m1∶m2=_______.
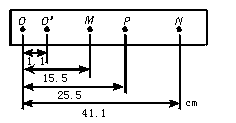
图2
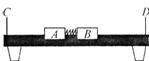12.（12分）气垫导轨是常用的一种实验仪器，它是利用气泵使带孔的导轨与滑块之间形成气垫，使滑块悬浮在导轨上，滑块在导轨上的运动可视为没有摩擦．我们可以用带竖直挡板C和D的气垫导轨和滑块A和B验证动量守恒定律，实验装置如图所示，采用的实验步骤如下：
a．用天平分别测出滑块A、B的质量mA、mB；
b．调整气垫导轨，使导轨处于水平；
c．在A和B间放入一个被压缩的轻弹簧，用电动卡销锁定，静止
放置在气垫导轨上；
d．用刻度尺测出A的左端至C板的距离L1；
e．按下电钮放开卡销，同时分别记录滑块A、B运动时间的计时器开始工作，当A、B滑块分别碰撞C、D挡板时计时结束，记下A，B分别到达C、D的运动时间t1和t2．
(1)实验中还应测量的物理量是 ．
(2)利用上述测量的实验数据，验证动量守恒定律的表达式是 ，上式中算得的A、B两滑块的动量大小并不完全相等，产生误差的原因是 ．
13.（13分）如图所示，在光滑的水平桌面上，静放着一质量为980g的长方形匀质木块，现有一颗质量为20g的子弹以300m/s的水平速度沿其轴线射向木块，结果子弹留在木块中没有射出，和木块一起以共同的速度运动。已知木块沿子弹运动方向的长度为10cm，子弹打进木块的深度为6cm。设木块对子弹的阻力保持不变。
（1）求子弹和木块的共同速度以及它们在此过程中所增加的内能。
（2）若子弹是以400m/s的水平速度从同一方向水平射向该木块的，则它能否射穿该木块？
14.（13分）如图所示，光滑水平面上有A、B、C三个物块，其质量分别为mA = 2.0kg，mB = 1.0kg，mC = 1.0kg．现用一轻弹簧将A、B两物块连接，并用力缓慢压缩弹簧使A、B两物块靠近，此过程外力做108J（弹簧仍处于弹性限度内），然后同时释放A、B，弹簧开始逐渐变长，当弹簧刚好恢复原长时，C恰以4m/s的速度迎面与B发生碰撞并粘连在一起．求：
（1）弹簧刚好恢复原长时（B与C碰撞前）A和B物块速度的大小．
（2）当弹簧第二次被压缩时，弹簧具有的最大弹性势能．
15.（15分）空间探测器从行星旁边绕过时，由于行星的引力作用，可以使探测器的运动速率增大，这种现象被称之为“弹弓效应”。在航天技术中，“弹弓效应”是用来增大人造小天体运动速率的一种有效方法．
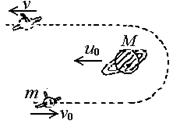（1）右图是“弹弓效应”的示意图：质量为m的空间探测器以相对于太阳的速度υ0飞向质量为M的行星，此时行星相对于太阳的速度为u0，绕过行星后探测器相对于太阳的速度为υ，此时行星相对于太阳的速度为u，由于mM，υ0、υ、u0、u的方向均可视为相互平行试写出探测器与行星构成的系统在上述过程中“动量守恒”及“始末状态总动能相等”的方程，并在m<<M的条件下，用υ0和u0来表示υ．
（2）若上述行星是质量为M＝5．67×1026kg的土星，其相对太阳的轨道速率u0 = 9.6km/s，而空间探测器的质量m＝150kg，相对于太阳迎向土星的速率υ0＝10.4km/s，则由于“弹弓效应”，该探测器绕过火星后相对于太阳的速率将增为多少？
（3）若探测器飞向行星时其速度υ0与行星的速度u0同方向，则是否仍能产生使探测器速率增大的“弹弓效应”？简要说明理由．
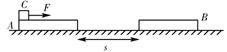16.（16分）如图所示，两个完全相同的质量分别为m的木块A、B置于水平地面上，它们的间距S＝2．88m．质量为2m，大小可忽略的滑块C置于A板的左端．C与A、B之间的动摩擦因数μ1 =
0．22，A、B与水平地面之间的动摩擦因数为μ2＝0.10，最大静摩擦力可认为等于滑动摩擦力．开始时，三个物体处于静止状态．现给C施加一个水平向右、大小为
mg 的力F，假定木板A、B碰撞时间极短且碰撞后粘连在一起，要使C最终不脱离木板，每块木板的长度至少应为多少？
17.（16分）在核反应堆里，用石墨作减速剂，使铀核裂变所产生的快中子通过与碳核不断的碰撞而被减速。假设中子与碳核发生的是弹性正碰，且碰撞前碳核是静止的。已知碳核的质量近似为中子质量的12倍，中子原来的动能为E0，试求：
（1）经过一次碰撞后中子的能量变为多少？
（2）若E0=1.76MeV，则经过多少次后，中子的能量才可减少到0.025eV。
18.（17分）.如图所示，水平传送带AB长L=8.3m，质量M=1kg的木块随传送带一起以v1=2m/s的速度向左运动（传送带的速度恒定不变），木块与传送带间的摩擦因数μ=0.5．当木块运动到传送带最左端A点时，一颗质量为m=20g的子弹以 vo=300m/s水平向右的速度正对入射木块并穿出，穿出速度为v2=50m/s，以后每隔1s就有一颗子弹射向木块．设子弹与木块的作用时间极短，且每次射入点不同，g=10m/s2．求：
（1）在木块被第二颗子弹击中前木块向右运动离A点的最大距离．
（2）木块在传送带上最多能被多少颗子弹子击中．
（3）在被第二颗子弹击中前，子弹、木块、传送带这一系统所产生的热能是多少？
参考答案
综合训练（A卷）
一.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| C | AD | BD | D | D | BC | BCD | AD | B | AC |
二.
11.（1）＞ （2）其末端切线水平 （3）D选项中，球1应从与C项相同高度滑下；P、M、N点应该是多次实验落地点的平均位置。F项中，应看
是否相等。
12 . 球1和球2的质量m1和m2，立柱的高h，桌面离地面的高H，m1
=m1
+m2c
13.解析：（1）F=(M+m)a
μmg=ma
F=μ(M+m)g=0.1×(3+1)×10N=4N
（2）小物体的加速度
木板的加速度
解得物体滑过木板所用时间
物体离开木板时的速度
（3）若要F作用时间最短，则物体离开木板时与木板速度相同。设F作用的最短时间为t1，物体在木板上滑行的时间为t，物体离开木板时与木板的速度为V
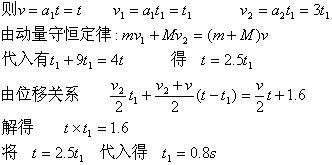
14.解析：（1）乙车与甲车碰撞过程中，小物体仍保持静止，甲、乙组成的系统动量守恒，
乙车速度为
，方向仍向左
（2）小物体m在乙上滑至两者有共同速度的过程中动量守恒：
有 
，
对小物体m是作匀加速直线运动，应用牛顿第二定律得a=μg
又有
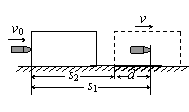
15.解析：子弹和木块最后共同运动，相当于完全非弹性碰撞。
从动量的角度看，子弹射入木块过程中系统动量守恒：
从能量的角度看，该过程系统损失的动能全部转化为系统的内能。设平均阻力大小为f，设子弹、木块的位移大小分别为s1、s2，
如图所示，有几何关系s1-s2=d ……（1）
对子弹据动能定理：
……（2）
对木块据动能定理：
……（3）
（2）、（3）相减得：
……（4）
（4）式的物理意义是：fžd恰好等于系统动能的损失；根据能量守恒定律，系统动能的损失应该等于系统内能的增加；可见
，即两物体由于相对运动而摩擦产生的热（机械能转化为内能），等于摩擦力大小与两物体相对滑动的路程的乘积（由于摩擦力是耗散力，摩擦生热跟路径有关，所以这里应该用路程，而不是用位移）。
由上式不难求得平均阻力的大小：
至于木块前进的距离s2，可以由以上（3）、（4）相比得出：
或从牛顿运动定律和运动学公式出发，也可以得出同样的结论。由于子弹和木块都在恒力作用下做匀变速运动，位移与平均速度成正比：
16.解析：（1）当A球与弹簧接触以后，在弹力作用下减速运动，而B球在弹力作用下加速运动，弹簧势能增加，当A、B速度相同时，弹簧的势能最大．
设A、B的共同速度为v，弹簧的最大势能为E，则A、B系统动量守恒，有
由机械能守恒 
联立两式得 
（2）设B球与挡板碰撞前瞬间的速度为vB，此时A的速度为vA
系统动量守恒
B与挡板碰后，以vB向左运动，压缩弹簧，当A、B速度相同（设为v共）时，弹簧势能最大
有 
得 
所以 
当弹簧恢复原长时与小球B挡板相碰，vB有最大值
，有
解得 ＝
即vB的取值范围为 
当vB＝
时Em有最大值为Em1＝
当vB＝
时，Em有最小值为Em2＝
17.解析：（1）全过程系统动量守恒，小物块在车左端和回到车右端两个时刻，系统的速度是相同的，都满足：mv0=(m+M) v；第二阶段初、末系统动能相同，说明小物块从车左端返回车右端过程中弹性势能的减小恰好等于系统内能的增加，即弹簧的最大弹性势能EP恰好等于返回过程的摩擦生热，而往、返两个过程中摩擦生热是相同的，所以EP是全过程摩擦生热Q的一半.又因为全过程系统的动能损失应该等于系统因摩擦而增加的内能， 所以
ΔEK=Q=2EP
而
， ∴
（2）B相对于车向右返回过程中小车的速度变化，则应该用牛顿运动定律来分析：刚开始向右返回时刻，弹簧对B的弹力一定大于滑动摩擦力，根据牛顿第三定律，小车受的弹力F也一定大于摩擦力f，小车向左加速运动；弹力逐渐减小而摩擦力大小不变，所以到某一时刻弹力和摩擦力大小相等，这时小车速度最大；以后弹力将小于摩擦力，小车受的合外力向右，开始做减速运动；B脱离弹簧后，小车在水平方向只受摩擦力，继续减速，直到和B具有向左的共同速度，并保持匀速运动
18解析:设第1号球与第2号球碰后的速度分别为v1和v2
由动量守恒定律得：
mv0=mv1+mv2 （1）
由能量关系可得
（2）
联解（1）（2）可得v2=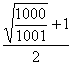
v0
由于每次碰撞所遵循的规律完全相同，分析归纳可得
经2001次碰撞后，第2002号球获得的速度为
v2002=(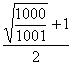
)2001v0 （3）
因为第2002号球恰能到圆轨道的最高点，所以对第2002号球，根据机械能守恒定律有
mv2+mg·2R （4）
在最高点有mg=m
（5）
联解（3）（4）（5）可得第1号球的初速度
v0 
3.69
综合训练（B卷）
一.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| BCD | CD | B | ABD | C | BC | B | BC | CD | AB |
二.
11. (1)天平；刻度尺 （2）4∶1
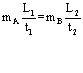
12：(1)B的右端至D板的距离L2 (2) ；测量质量、时间、距离等存在误差，由于阻力、气垫导轨不水平等造成误差．(只要答对其中两点即可)
13.解析：（1）设子弹的初速度为v0，射入木块的共同速度为v.以子弹和木块为系统，由动量守恒定律有
（2分）解得
此过程系统所增加的内能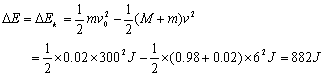
（2）设以v0′=400m/s的速度刚好能够射穿材质一样厚度为d′的另一个木块.则对以子弹和木块组成的系统，由动量守恒定律有：
此过程系统所损耗的机械能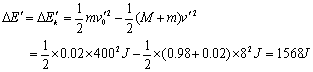
由功能关系有
两式相比即有
于是有
因为d′>10cm，所以能够射穿此木块.
14.解析：（1）弹簧刚好恢复原长时，A和B物块速度的大小分别为υA、υB．
由动量守恒定律有：0 = mAυA - mBυB
此过程机械能守恒有：Ep = mAυ
+mBυ
代入Ep＝108J，解得：υA＝6m/s，υB = 12m/s，A的速度向右，B的速度向左．
（2）C与B碰撞时，设碰后B、C粘连时速度为υ′，据C、B组成的系统动量守恒
有：mBυB -mCυC = （mB+mC）υ′，代入数据得υ′ = 4m/s，υ′的方向向左．
此后A和B、C组成的系统动量守恒，机械能守恒，当弹簧第二次压缩最短时，弹簧具有的弹性势能最大，设为Ep′，且此时A与B、C三者有相同的速度，设为υ，则有：
动量守恒：mAυA -（mB+mC）υ′ = （mA+mB+mC）υ，代入数据得υ = 1m/s，υ的方向向右．
机械能守恒：mAυ+（mB+mC）υ′2 = Ep′+（mA+mB+mC）υ2，代入数据得
E′p＝50J．
15.解析：设两物体质量分别为m1、m2，碰撞前速度分别为υ10、υ20，碰撞后速度分别为υ1，υ2，且碰撞是弹性正碰，则有：
动量守恒即m1υ10+m2υ20 = m1υ1+m2υ2 （1）
动能守恒即m1υ
+m2υ
= m1υ
+m2υ
（2）
将（1）式变形有：m1（υ10 -υ1） = m2（υ2- υ20） （3）
将（2）式变形有：m1（υ10 -υ1）（υ10+υ1） = m2（υ2 -υ20）（υ2+υ20） （4）
将（4）÷（3）有：υ10+υ1 = υ2+υ20 （5）
由（1）和（5）解得：υ1 = 
υ10+
υ20，
υ2 = 
υ10+
υ20．
（1）以探测器初始时速度υ0的反方向为速度的正方向，有
得
∵ m＜＜M ∴ 
（2）代入数据，得 
km/s
（3）不能。如u0与题中反向，则在上述坐标系中，u0＜0，要使探测器追上并绕过行星，应有
＞
，因此，
＜
，可见不能使探测器速率增大。
16.解析：A、C之间的滑动摩擦力大小为f1，f1 = μ1mcg = 0.44mg，A与水平地面之间的滑动摩擦力大小为f2，f2 = μ2（mA+mC）g = 0.3mg，外力F = mg = 0．4mg可见F＜f1，F＞f2，即首先A和C之间保持相对静，在F的作用下一起向右做加速运动．设A与B碰撞前A、C的速度大小为υ1，由动能定理有：（F-f2）s = （mA+mC）υ 代入数据得：υ1 = 0．8
m/s
A、B两木板的碰撞瞬间，内力的冲量远大于外力的冲量，由动量守恒定律，设A、B碰后一起运动的速度为υ2，则有：mAυ1 = （mA+mB）υ2 得υ2 = 
= 0．4m/s
碰撞后C与A、B之间有相对滑动，此时A、B与地面间滑动摩擦力大小为f3，f3＝μ2（mA+mB+mC）g = 0．4mg，可见F＝f3，即三物体组成的系统受合外力为零，动量守恒，设它们达到的共同速度为υ3，此时A、B向前滑动的距离为s1，C恰好滑到B板的右端，此后三者一起做匀速运动，C不会脱离木板，设对应的木块长度为l．
由动量守恒有：mcυ1+（mA+mB）υ2 = （mC+mA+mB）υ3 得υ3 = 0．6m/s
对A、B整体，由动能定理有：f1s1-f3s1 = （mA+mB）（υ
-υ），得s1 = 1.5m
对C，由动能定理有：F（2l+s1）- f1（2l+s1） = mC（υ- υ），得l = 0.3m
17.解析：（1）弹性正碰遵循动量守恒和能量守恒两个规律。设中子的质量m，碳核的质量M。有：
由上述两式整理得 
则经过一次碰撞后中子的动能
（2）同理可得 
……
设经过n次碰撞，中子的动能才会减少至0.025eV，即En=0.025eV，E0=1.75MeV。
解上式得 n≈54
18.解析: (1)第一颗子弹射入并穿出木块过程中，由动量守恒：
mv0－Mv1=mv2+Mv1′
解得：v1′=3m/s
木块向右做减速运动，其加速度大小：
m/s2
木块速度减小为零所用时间为：
s<1s 所以木块在被第二颗子弹击中前向右运动速度为零时离A点最远，移动的距离为：
m
(2)在第二颗子弹射中木块前，木块再向左做加速运动，时间：
t2=1s－0.6s=0.4s
速度增大为：v'2=at2=2m/s（恰与传递带同速）
向左移动的位移为:
m
所以两颗子弹击中木块的时间间隔内，木块总位移：
s0=s1－s2=0.5m，方向向右
设木块在传送带上最多能被n颗子弹击中，则：
解得：n＝16
(3)第一颗子弹击穿木块过程中产生的热量为：
木块向右减速运动过程中相对传送带的位移为：
产生的热量为：
木块向左加速运动过程中相对传送带的位移为
，
产生的热量为：
所以，在第二颗子弹击中前,系统产生的总热能为：
