高三物理力与运动大题格式训练
请注意：解答应写出必要的文字说明、方程式和重要演算步骤,只写出最后答案的不得分.有数值计算的题,答案中必须明确写出数值和单位
1、假定神舟5号飞船在发射后3s内竖直上升了180m，上升过程是初速为零的匀加速直线运动，求飞船内质量为60kg的宇航员对座椅的压力多大？g取10m/s2
2、如图所示，物体从光滑斜面上的A点由静止开始下滑，经过B点后进入水平面（设经过B点前后速度大小不变），最后停在C点。每隔0.2秒钟通过速度传感器测量物体的瞬时速度，下表给出了部分测量数据。（重力加速度g＝10m/s2）
求：
（1）斜面的倾角a
（2）物体与水平面之间的动摩擦因数m
（3）t＝0.6s时的瞬时速度v
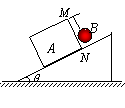
3、如图所示，固定在水平面上的斜面其倾角θ=37º，长方体木块A的MN面上钉着一颗小钉子，质量m=1.5kg的小球B通过一细线与小钉子相连接，细线与斜面垂直．木块与斜面间的动摩擦因数μ=0.50．现将木块由静止释放，木块将沿斜面下滑．求在木块下滑的过程中小球对木块MN面的压力大小．（取g=10m/s2，sin37º=0.6，cos37º=0.8）
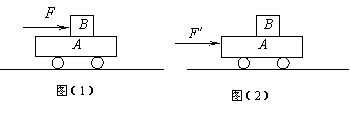4、如图所示，在光滑水平面上有一小车A，其质量为
kg，小车上放一个物体B，其质量为
kg，如图（1）所示。给B一个水平推力F，当F增大到稍大于3.0N时，A、B开始相对滑动。如果撤去F，对A施加一水平推力F′，如图（2）所示，要使A、B不相对滑动，求F′的最大值
5、质量为40kg的雪撬在倾角θ=37°的斜面上向下滑动（如图甲所示），所受的空气阻力与速度成正比。今测得雪撬运动的v-t图像如图7乙所示，且AB是曲线的切线，B点坐标为（4，15），CD是曲线的渐近线。试求空气的阻力系数k和雪撬与斜坡间的动摩擦因数μ。
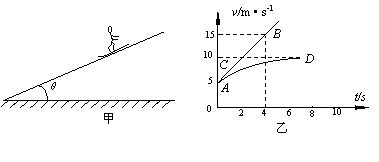
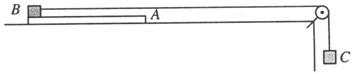
6、如图所示，在光滑的桌面上叠放着一质量为mA=2.0kg的薄木板A和质量为mB=3 kg的金属块B．A的长度L=2.0m．B上有轻线绕过定滑轮与质量为mC=1.0 kg的物块C相连．B与A之间的滑动摩擦因数 µ =0.10，最大静摩擦力可视为等于滑动摩擦力．忽略滑轮质量及与轴间的摩擦．起始时令各物体都处于静止状态，绳被拉直，B位于A的左端（如图），然后放手，求经过多长时间t后 B从 A的右端脱离（设 A的右端距滑轮足够远）（取g=10m/s2）．
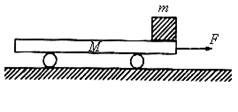
7、如图质量
的小车停放在光滑水平面上，在小车右端施加一水平恒力F=8N。当小车向右运动速度达到3m/s时，在小车的右端轻放一质量m=2kg的小物块，物块与小车间的动摩擦因数
，假定小车足够长，问：
（1）经过多长时间物块停止与小车间的相对运动？
（2）小物块从放在车上开始经过
所通过的位移是多少？（g取
）
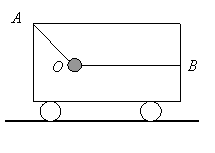
8、如图，小车在水平面上以5m/s的速度向右做匀速直线运动，车厢内用OA、OB两细绳系住一个质量为2kg的物体，OA与竖直方向夹角为θ=37°,OB是水平的。后来小车改做匀减速运动，并经1.25m的位移停下来, 求
(1)车在匀速运动的过程中，两绳的拉力TA、TB各是多少? (sin37º=0.6)
(2)车在匀减速运动的过程中，两绳的拉力TA、TB各是多少? (g取10m/s2 ）
9、如图所示，在水平面上有一质量为m的物体，在水平拉力作用下由静止开始运动一段距离后到达一斜面底端，这时撤去外力物体冲上斜面，上滑的最大距离和在平面上移动的距离相等，然后物体又沿斜面下滑，恰好停在平面上的出发点。已知斜面倾角θ＝300，斜面与平面上的动摩擦因数相同，求物体开始受的水平拉力F？
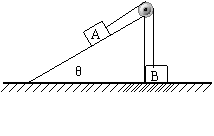
10、如图，一固定的楔形木块，其斜面的倾角为θ=300，另一边与地面垂直，顶上有一定滑轮，一柔软的细线跨过[定滑轮，两端分别与物块A和B连结，A的质量为4m，B的质量为m，开始时将B按在地上不动，然后放开手，让A沿斜面下滑而B上升，物块A与斜面间无摩擦。设当A沿斜面下滑S距离后，细线突然断了。求物块B上升的最大高度。
 |
参考答案
1、解：由
得
①
对宇航员，由牛顿运动定律得
②
由牛顿第三定律得
宇航员对座椅的压力是3000N ③
2、（1）由前三列数据可知物体在斜面上匀加速下滑时的加速度为a1＝＝5m/s2，
mg sin a＝ma1，可得：a＝30°，
（2）由后二列数据可知物体在水平面上匀减速滑行时的加速度大小为a2＝＝2m/s2，
mmg＝ma2，可得：m＝0.2，
（3）由2＋5t＝1.1＋2（0.8－t），解得t＝0.1s，即物体在斜面上下滑的时间为0.5s，
则t＝0.6s时物体在水平面上，其速度为v＝v1.2＋a2t＝2.3 m/s。
3、以木块和小球整体为研究对象，设木块的质量为M，下滑的加速度为a，沿斜面方向，根据牛顿第二定律有：
（M＋m）gsin37º－μ（M＋m）gcos37º=（M＋m）a
解得：a=g（sin37º－μcos37º）=2m/s2
以小球B为研究对象，受重力mg，细线拉力T和MN面对小球沿斜面向上的弹力FN，沿斜面方向，根据牛顿第二定律有：
mgsin37º－FN=ma
解得：FN=mgsin37º－ma=6N．
由牛顿第三定律得，小球对木块MN面的压力大小为6N．
4、根据图（1），设A、B间的静摩擦力达到最大值
时，系统的加速度为
.根据牛顿第二定律有： 
①
②
代入数值联立解得：
③
根据图（2）设A、B刚开始滑动时系统的加速度为
，根据牛顿第二定律有：
④ 
⑤
联立解得：
⑥
5、由牛顿运动定律得：
由平衡条件得：
由图象得：A点，vA=5m/s，加速度aA＝2.5m/s2；
最终雪橇匀速运动时最大速度vm=10m/s，a＝0
代入数据解得：μ=0.125 k=20N·s/m
6、以桌面为参考系，令aA表示A的加速度，aB表示B、C的加速度，sA和sB分别表示 t时间 A和B移动的距离，则由牛顿定律和匀加速运动的规律可得
mCg-µmBg=（mC+mB）aB
µ mBg=mAaA
sB=
aBt2
sA=aAt2
sB-sA=L
由以上各式，代入数值，可得
t=4.0s
7、依据题意，物块在小车上停止运动时，物块与小车保持相对静止，应具有共同的速度。设物块在小车上相对运动时间为t，物块、小车受力分析如图：
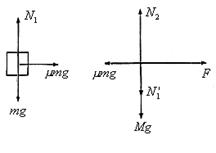物块放上小车后做初速度为零加速度为
的匀加速直线运动，小车做加速度为
匀加速运动。
由牛顿运动定律：
物块放上小车后加速度：
小车加速度：
由
得：
（2）物块在前2s内做加速度为的匀加速运动，后1s同小车一起做加速度为的匀加速运动。
以系统为研究对象：
根据牛顿运动定律，由
得：
物块位移
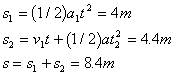
8解:匀速运动时:
TA sinθ=TB ①
TAcosθ= mg ②
得TA=25N TB=15N
(2)匀减速时,有向左的加速度,设B绳上弹力为0时(临界条件)加速度为a
TA sinθ=mg ③
TAcosθ=ma0 ④
则:a0=gtanθ
因为a=g>gtanθ所以小球飞起来,TB=0 ,设此时A绳与竖直方向夹角为a
TA sina=mg ⑤
TAcosa=ma ⑥
解得TA=28.2N(也可用勾股定理解)
9、解：设物体与地面的摩擦因数为μ，在拉力作用下运动到斜面底端时的速度为v0。
向右加速过程的加速度为： 
①（1分）
其通过的位移为： 
②（1分）
物体沿斜面上滑过程的加速度为：
③（1分）
沿斜面上滑过程有： 
④（1分）
物体下滑过程的加速度为：
⑤（1分）
设物体下滑到斜面底端时的速度为v,下滑过程有：
⑥（1分）
向左运动过程的加速度为： 
⑦（1分）
向左运动过程有： 
⑧（1分）
由以上8式解得：
（2分）
10、B先和A一起匀加速直线运动，
对A：
对B：
解得
匀加速的末速度
B接下来作竖直上抛运动，继续上升的高度
