高三物理上学期十月月考试卷
一．（50分）选择题. 本大题共10小题，每小题5分. 每小题给出的四个答案中，至少有一个是正确的. 把正确答案全选出来，并将正确答案前面的字母填写在题后的方括号内. 每一小题全选对的得5分；选对但不全，得部分分；有选错或不答的，得0分. 填写在方括号外的字母，不作为选出的答案.
1．根据牛顿运动定律，以下选项中正确的是（ C ）
A．人只有在静止的车厢内，竖直向上高高跳起后，才会落在车厢的原来位置．
B．人在沿直线匀速前进的车厢内，竖直向上高高跳起后，将落在起跳点的后方．
C．人在沿直线加速前进的车厢内，竖直向上高高跳起后，将落在起跳点的后方．
D．人在沿直线减速前进的车厢内，竖直向上高高跳起后，将落在起跳点的后方．
2．在一根轻绳的两端各拴一个小铁球，一人用手拿住绳上端的小球站在三层楼的阳台上，放手让小球自由下落，两球落地时间差为
，如果站在四楼阳台上，重复上述实验，则两球落地时间差为
，则 （ C ）
A．= B．> C．< D．由于具体变量不知，无法比较
3．a、b和c是三个一样大小的球，a为实心木球，b为实心铁球，c为空心铁球，都从静止起下落，它们受到的空气阻力大小相同，则 ( BD)
A.a球加速度最大. B.b球加速度最大.
C.c球加速度最大. D.b球落地所需时间最短.
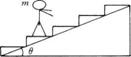4．如图所示，质量为m的人在自动扶梯上，已知鞋底与扶梯间的滑动摩擦系数为µ，扶梯与水平面问的夹角为θ，假定人随扶梯以加速度a一起向上加速运动，这时人受到的摩擦力大小是 ( A )
A. macosθ. B.μmg. C.μm(g+asinθ). D. ma
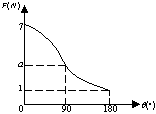
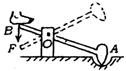5．如图所示，为南方少数民族常用的一种舂米工具。O为固定转动轴，重锤为A。脚踩在左端B处，可以使重锤升高，放开脚重锤落下打击稻谷。若脚用力方向始终竖直向下且转动保持平衡状态，则在重锤升起过程中，脚踩B端向下的力F和力矩M将：（ C ）
A F增大，M增大； B F先增大后减少，M不变；
C F不变，M先增大后减小； D F不变，M先减小而增大。
6．一个物体在几个共点力的作用下，保持平衡状态，如果撤去其中一个力F1，而其余力保持不变，关于该物体的运动，下列说法中正确的是 （ BC ）
A 可能沿着F1的方向做匀加速直线运动
B 可能沿着F1的反方向做匀加速直线运动
C 可能做匀变速曲线运动
D 可能做匀速圆周运动
 |
7．下面四个图像依次分别表示四个物体A、B、C、D的加速度、速度、位移和滑动摩擦力随时间变化的规律。其中物体可能受力平衡的是（ CD ）
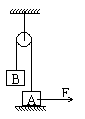
8．如图示，在台秤的托盘上放着一个支架，支架上面挂有一个电磁铁A，其正下方有铁块B，现接通电磁铁的电源，则： （ AB ）
A.当铁块被吸起离开台秤的过程中，台秤示数变大
B.当铁块被吸引，但仍保持静止，台秤示数不变
C.只要铁块被吸引、不论它是否运动，台秤示数都变大
D.不论铁块是否被吸引，只要它静止，台秤示数都变小
9．为了研究超重与失重现象，某同学把一体重秤放在电梯的地板上，他站在体重秤上随电梯运动并观察体重秤示数的变化情况．下表记录了几个特定时刻体重秤的示数．（表内时间不表示先后顺序）：
| 时 间 | t0 | t1 | t2 | t3 |
| 体重秤示数（kg） | 45.0 | 50.0 | 40.0 | 45.0 |
若已知t0时刻电梯处于静止状态，则： （ C D ）
(A) t1和t2时刻该同学的质量并没有变化，但所受重力发生变化．
(B) t1和t2时刻电梯的速度一定不为零．
(C) t1和t2时刻电梯的加速度一定是大小相等、方向相反．
(D) t3时刻电梯一定处于平衡状态．
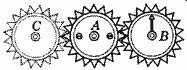10．如图所示，Ａ、Ｂ是两只相同的齿轮，Ａ被固定不能转动，若Ｂ齿轮绕Ａ齿轮运动半周，到达图中的Ｃ位置，则Ｂ齿轮上所标出的竖直向上的箭头所指的方向是 （ A ）
Ａ．竖直向上 Ｂ．竖直向下
Ｃ．水平向左 Ｄ．水平向右
二．（40分）填空题. （本大题共8小题，11—16题，每空格2分。17、18题每题4分）
11．F1和F2的合力大小随着他它们的夹角θ变化的关系如图所示（F1、F2的大小均不变，且F1>F2）。则可知F1的大小为＿4＿N，F2的大小为＿3＿N，a的值为＿5＿N。
12．一气球重10N，受空气浮力16N，用绳将其栓住，由于风力水平作用于气球，使绳偏离竖直方向37°角，则气球受绳的拉力是 7.5 N,受水平风力是 4.5 N。
13．一物体恰能在一个斜面体上沿斜面匀速下滑，可以证明此时地面对斜面的摩擦力为零．若用沿斜面向下的力推此物体，使物体加速下滑（如图所示），则斜面受到地面的摩擦力 为零 ；若将该力的方向改为竖直向下作用在物体上，使物体下滑，则斜面受到地面的摩擦力 为零 ．（选填“水平向左”、“水平向右”或“为零” ）
14．一船在静水中的划行速率为3m/s，要横渡一条宽30m、流速为5m/s的河流。此船渡河的最短时间为 10 s，此时船渡河的航程为
m.。此船渡河的最短航程为
50 m.
|
|
|
|
15．如图所示,A、B两物体通过定滑轮以细线相连接。A在拉力F作用下缓慢向右运动，物体B上升。则在此过程中A受地面支持力N将 增大 ，摩擦力f将 增大 ，绳中张力T将 不变 ，拉力F将 增大 。（填增大、减少或不变）
 |
16．图a表示用水平恒力F拉动水平面上的物体，使其做匀加速运动．当改变拉力的大小时，相对应的匀加速运动的加速度a也会变化，a和F的关系如图b所示，则该物体的质量是 0.5 kg，物体与水平面间的动摩擦因数是 0.2 ．
|
|
|
|
|
|
17．一架托盘天平没有游砝码，最小砝码为100mg。用这台已调好的天平称量某物的质量，当右盘加26.20g砝码时，天平指针向左偏1小格，(如图中实线)如果再加上100mg砝码，天平指针向右偏1.5小格，(如图中虚线)则该物体质量为 26.24 g。
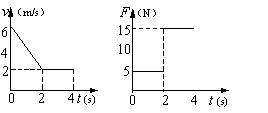18．一物体在粗糙的水平面上做直线运动，运动速度v及所受水平拉力F随时间变化的图线如图所示，由此可知物体与地面间的动摩擦因数为μ＝__0.3___
。
三．（60分）计算题.
19．（10分）在一个足够长的固定斜面上，从顶点A平抛一小球，当抛出的初速度为
时，落至斜面上的D点，AD=S，求当抛出的初速度为′时，落至斜面上的位置离A点的距离。
19.解：设斜面倾角为
。
根据
解得 
…（3分）所以 
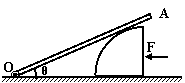
20、(12分）如图所示，横截面为四分之一圆（半径为R）的柱体放在水平地面上，一根匀质木棒OA长为3R，重为G。木棒的O端与地面上的铰链连接，木棒搁在柱体上，各处摩擦均不计。现用一水平推力F作用在柱体竖直面上，使柱体沿着水平地面向左缓慢移动。问：
（1）当木棒与地面的夹角θ = 30°时，柱体对木棒的弹力多大？
（2）此时水平推力F多大？
（3）在柱体向左缓慢移动过程中，柱体对木棒的弹力及水平推力F分别如何变化？
20．解：（1）利用力矩平衡：
N＝0.75G （3分）
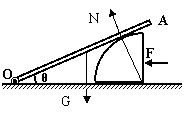（2）以四分之一圆为研究对象，将N正交分解得：
F＝Nｓｉｎθ＝0.375G （3分）
（3）由
得：
（3分）
当圆柱体向左推时θ角增大，故N增大，
又F＝
，所以F也在增大。 （3分）
21．（12分）如图所示，物体从光滑斜面上的A点由静止开始下滑，经过B点后进入水平面（设经过B点前后速度大小不变），最后停在C点。每隔0.2秒钟通过速度传感器测量物体的瞬时速度，下表给出了部分测量数据。（重力加速度g＝10m/s2）
求：
|
|
（1）斜面的倾角a；
（2）物体与水平面之间的动摩擦因数m；
（3）t＝0.6s时的瞬时速度v。
|
|
21．解：（1）由前三列数据可知物体在 斜面上匀加速下滑时的加速度为
a1＝＝5m/s2 （2分）
mg sin a＝ma1，可得：a＝30°（2分），
（2）由后二列数据可知物体在水平面上匀减速滑行时的加速度大小为
a2＝＝2m/s2， （2分）
mmg＝ma2，可得：m＝0.2 （2分），
（3）设物体在斜面上下滑的时间为t1。
得5t1＝1.1＋2（1.2－t1），解得t1＝0.5s，（2分）
则t＝0.6s时物体在水平面上，其速度为v＝a1 t1-a2（t- t1）＝2.3 m/s。（2分）
22．（12分）在倾角为α的斜面上，一条质量不计的皮带一端固定在斜面上端，另一端绕过一中间有一圈凹槽的圆柱体，并用与斜面夹角为β的力拉住，使整个装置处于静止状态，如图所示。不计一切摩擦，圆柱体质量为m，求拉力F的大小和斜面对圆柱体的弹力N的大小。
22．解：将拉力F沿斜面和垂直于斜面方向进行分解。
沿斜面方向： F cosb＋F＝mg sina （1）（3分）
沿垂直于斜面方向： F sinβ＋N＝mg cos α （2）（3分）
由（1）得F＝mg ＝30´ N＝10 N（4）（3分）
代入（2），解得
N＝mg cosa－F sinb＝（30´0.8－10´0.6）N＝18 N （3分）
23．（14分）甲、乙两质点同时开始在彼此平行且靠近的两水平轨道上同向运动，甲在前，乙在后，相距s，甲初速度为零，加速度为a，做匀加速直线运动；乙以速度v0做匀速运动，关于两质点在相遇前的运动。
某同学作如下分析：
设两质点相遇前，它们之间的距离为△s，则
，当
时，两质点间距离△s有最小值，也就是两质点速度相等时，两质点之间距离最近。
你觉得他的分析是否正确？如果认为是正确的，请求出它们的最小距离；如果认为是不正确的，请说明理由并作出正确分析。
23．解：不正确。 （3分）
在两质点相遇之前，它们之间的距离Δs也可能不断减小，直至Δs＝0（相遇），而不存在变小后变大的情况，这完全取决于两质点之间的初始距离s与v0、a之间的大小关系
（3分）
由 s＝v0t－
可解得：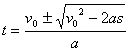
可见，若v02＝2as 即
则
（2分）
当t≤
时，甲乙之前的距离始终在减小，直至相遇，（最小距离Δ s＝0），不会出现Δs有最小值的情况。
（2分）
当v0<2as，即s>
时，甲与乙不可能相遇，在t<时，两质点距离会出现先变小后变大的情况，当t=时，两质点之间的距离最近，：Δ s min＝s－
（4分）