简谐运动
一、本周内容:
1、简谐运动
2、振幅、周期和频率
二、本周重点:
1、简谐运动过程中的位移、回复力、加速度和速度的变化规律
2、简谐运动中回复力的特点
3、简谐运动的振幅、周期和频率的概念
4、关于振幅、周期和频率的实际应用
二、知识点要点:
1、机械振动
(1)定义:物体在平衡位置附近所做的往复运动,叫做机械振动,简称振动。
(2)产生振动的条件:
①物体受到的阻力足够小
②物体受到的回复力的作用
手施力使水平弹簧振子偏离平衡位置,感到振子受到一指向平衡位置的力,它总要使振子返回平衡位置,所以叫做回复力。回复力是根据力的作用效果命名的。回复力可以是弹力,也可以是其他的力,或几个力的合力,或某个力的分力。
(3)机械振动是一种普遍的运动形式,大至地壳振动,小至分子、原子的振动。
2、简谐运动
(1)定义:物体在跟位移的大小成正比,并且总指向平衡位置的回复力作用下的运动,叫简谐运动
(2)条件:物体做简谐运动的条件是F=-kx,即物体受到的回复力F跟位移大小成正比,方向跟位移方向相反。
(3)对F=-kx的理解:对一般的简谐运动,k是一个比例常数,不同的简谐运动,K值不同,k是由振动系统本身结构决定的物理量,在弹簧振子中,k是弹簧的劲度系数。
3、简谐运动的特点
(1)回复力:物体在往复运动期间,回复力的大小和方向均做周期性的变化,物体处在最大位移处时的回复力最大,物体处于平衡位置时的回复力最小(为零),物体经过平衡位置时,回复力的方向发生改变。
(2)加速度:由力与加速度的瞬时对应关系可知,回复力产生的加速度也是周期性变化的,且与回复力的变化步调相同。
(3)位移:物体做简谐运动时,它的位移(大小和方向)也是周期性变化的,为研究问题方便,选取平衡位置位移的起点,物体经平衡位置时位移的方向改变。
(4)速度:简谐运动是变加速运动,速度的变化也具有周期性(包括大小和方向),物体经平衡位置时的速度最大,物体在最大位移处的速度为零,且物体的速度方向改变。
4、振幅(A)
(1)定义:振动物体离开平衡位置的最大距离,单位:m
(2)作用:描述振动的强弱。
(3)振幅和位移的区别:对于一个给定的振动,振子的位移是时刻变化的,但振幅是不变的,位移是矢量,振幅是标量,它等于最大位移的大小。
5、周期和频率
(1)周期(T):振动物体完成一次全振动所需要的时间,单位:s
(2)频率(f):单位时间内完成全振动的次数,单位:Hz
(3)一次全振动(往返一次):振动物体经过一段时间的运动,位移、加速度、速度都恢复为原来的状态,即完成一次全振动。如振子从O→B→O→C→O或从B→O→C→O→B等。
![]() (4)周期与频率的关系:f=1/T 1Hz=1/s=s-1
(4)周期与频率的关系:f=1/T 1Hz=1/s=s-1
(5)作用:描述振动的快慢
(6)测量仪器:秒表、节拍器
6、固有周期和固有频率
(1)弹簧振子的周期由振动系统中振子的质量与劲度系数决定,而与振幅无关。
(2)公式:![]()
(3)简谐运动的周期和频率由振动系数本身的性质决定,因此叫做固有周期和固有频率。
四、典型例题:
例1、如图所示,在光滑水平面上,用两根劲度系数分别为k1、k2的轻弹簧系住一个质量为m的小球,开始时,两弹簧均处于原长,后使小球向左偏离x后放手,可以看到小球将在水平面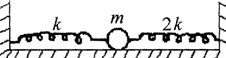 上作往复振动,试问小球是否作简谐运动?
上作往复振动,试问小球是否作简谐运动?
分析:
为了判断小球的运动性质,需要根据小球的受力情况,找出回复力,确定它能否写成F=-kx的形式。
解析:
以小球为研究对象,竖直方向处于力平衡状态,水平方向受到两根弹簧的弹力作用,设小球位于平衡位置O左方某处时,偏离平衡位置的位移为x,则
左方弹簧受压,对小球的弹力大小为F1=k1x,方向向右。
右方弹簧被拉伸,对小球的弹力大小为F2=k2x方向向右。
小球所受回复力等于两个弹力的合力,其大小为F=F1+F2=(k1+k2)x,方向向右,
令k=k1+k2,上式可写成F=kx
由于小球所受回复力的方向与位移x的方向相反,考虑方向后,上式可表示为F=-kx所以,小球将在两根弹簧的作用下,沿水平面简谐运动。
说明:
由本题可归纳出判断物体是否作简谐运动的一般步骤:确定研究对象(整个物体或某一部分)→分析受力情况→找出回复力→表示成F=-kx的形式(可以先确定F的大小与x的关系,再定性判断方向)。
例2、物体做简谐运动时,下列判断中正确的是( )
A、在平衡位置加速度最大。
B、在平衡位置速度最大。
C、在运动路径两端速度最大。
D、在运动路径两端加速度最小。
分析:
物体做简谐运动时受到的回复力为F=-kx
根据牛顿第二定律,物体在振动过程中的加速度为![]()
即加速度的大小与位移成正比,加速度的方向与位移方向相反。
物体在平衡位置时,位移x=0,加速度a=0。
在运动路径两端时,位移最大,加速度也最大,所以A、D都错。
物体在运动路径两端时,速度都等于零,C错。
从两端向平衡位置运动时,物体作加速度大小在变小、速度大小在变大的变加速运动,至平衡位置时速度达最大。B正确。
答:B。
例3、一个弹簧振子,第一次用力把弹簧压缩x后开始振动,第二次把弹簧压缩2x后开始振动,则两次振动的周期之比和最大加速度的大小之比分别为( )
A、1:2,1:2 B、1:1,1:1 C、1:1,1:2 D、1:2,1:1
分析:
简谐运动物体的周期只决定于振动系统固有的性质,对弹簧振子则由振子的质量与弹簧的劲度系数决定,与起振时的初始位移大小无关。所以周期之比为1:1。弹簧振子在振动中所受的回复力为F=-kx,其加速度![]() ,位移越大,振子的加速度也越大,所以两情况中的最大加速度之比为1:2。
,位移越大,振子的加速度也越大,所以两情况中的最大加速度之比为1:2。
答:C。
例4、如图所示,一个作简谐运动的质点,先后以同样大小的速度通过相距10cm的A、B两点,历时0.5s,过B点后再经过t=0.5s质点以方向相反、大小相同的速度再次通过B点,则质点振动的周期是( )。
![]() A、0.5s B、1.0s C、2.0s D、4.0s
A、0.5s B、1.0s C、2.0s D、4.0s
分析:
根据题意,由振动的对称性可知:AB的中点(设为O)为平衡位置,A、B两点对称分布于O点两侧;质点从平衡位置O向右运动到B的时间应为
![]()
质点从B向右到达右方极端位置(设为D)的时间![]()
所以,质点从O到D的时间![]()
所以T=2s。
答:C。
说明:
本题的关键是认识振动的对称性,如图所示,设C、D为质点振动中左方和右方的极端位置,则由对称性可知:
![]() 质点从B→D→B的时间一定等于质点从A→C→A的时间,即tBDB=tACA=0.5s
质点从B→D→B的时间一定等于质点从A→C→A的时间,即tBDB=tACA=0.5s
所以,质点振动周期T=tAB+tBDB+tBA+tACA=2s
例5、如图所示,竖直悬挂的轻弹簧下端系着A、B两球,其质量mA=0.1kg、mB=0.5kg。 静止时弹簧伸长15cm,若剪断A、B间的细线,则A作简谐运动时的振幅和最大加速度为多少? g=10m/s2。
g=10m/s2。
分析:
剪断A、B间的细线后,A球成为竖直悬挂的弹簧振子,其振幅由它所处的初始 状态决定,振动中的最大加速度由振子受到的最大回复力用牛顿第二定律可算出。
解答:
由两球静止时的力平衡条件,得弹簧的劲度系数为
![]() =40N/m。
=40N/m。
剪断A、B间细线后,A球静止悬挂时的弹簧的伸长量为
![]() =2.5cm。
=2.5cm。
弹簧下端的这个位置就是A球振动中的平衡位置。
悬挂B球后又剪断细线,相当于用手把A球下拉后又突然释放,刚剪断细线时弹簧比静止悬挂A球多伸长的长度就是振幅,即A=x-xA=15cm-2.5cm=12.5cm。
振动中A球的最大加速度为
![]() =50m/s2。
=50m/s2。
五、练习题:
1、使物体产生振动的必要条件是( )
A、物体所受到的各个力的合力必须指向平衡位置。
B、物体受到阻力等于零。
C、物体离开平衡位置后受到回复力的作用,物体所受的阻力足够小。
D、物体离开平衡位置后受到回复力F的作用,且F=-kx(x为对平衡位置的位移)。
2、如图所示,小球以O点为平衡位置,A、B为两极端位置往复振动,在某位置P的位移( )。
A、从B点返回P时,用线段BP表示,方向向P。
B、只有从O向P运动时,才作OP表示,方![]() 向向P。
向向P。
C、用PO表示,方向向O。
D、用OP表示,方向向P。
3、关于简谐运动的有关物理量,下列说法中错误的是( )
A、回复力方向总是指向平衡位置。
B、向平衡位置运动时,加速度越来越小,速度也越来越小。
C、加速度和速度方向总是跟位移方向相反。
D、速度方向有时跟位移方向相同,有时相反。
4、作简谐运动的物体每次通过同一位置时,都具有相同的( )
A、加速度 B、动量 C、动能 D、位移 E、回复力 F、速度
5、第2题图中,小球受到回复力最大的位置是________;小球加速度最大的位置是_______,速度最大的位置是________,小球在位置A的加速度方向________;小球在位置P的加速度方向________。
6、关于简谐运动的以下几个说法中,错误的是( )
A、质点从平衡位置起第1次到最大位移处所需时间为T/4(T是周期)。
B、质点走过一个振幅那么长的路程用的时间总是T/4。
C、质点在T/4时间内走过的路程恒等于一个振幅的长度。
D、质点在T/4时间内走过的路程可以大于、也可以小于一个振幅的长度。
7、将一个水平方向的弹簧振子从它的平衡位置向旁边拉开5cm,然后无初速释放,假如这振子振动的频率为5Hz,则振子在0.8s内通过的路程是________。
8、一质点在O点附近做简谐运动,它离开O点向M点运动,3s后,第一次到达M点;再经过2s,第二次到达M点,则这个质点还要经过________s,第三次到达M点。
六、参考答案:
1、C.
提示:D是简谐运动的条件。
2、D. 3、B,C。 4、A,C,D,E。
5、A和B,A和B,O。指向O。指向O。
6、B,C. 7、0.8m。 8、14。