第一章 数的有关问题
第一节 数位及数的表示
1.在110～130这21个数中，将所有奇数的十位与个位之间加一个小数点；再将所有偶数的百 位与十位之间加一个小数点，经变换后的21个数之和是 .
2.把一个两位数的个位数字与十位数字交换后得到一个新数，它与原数相减的差恰好等于两 个相同数的积(不为零)，则满足以上条件的原两位数中最小的一个是 .
3.一个三位数，各位数字分别为a、b、c，它们互不相等，且都不为零.用a、b、c共可排得 六个不同的三位数，其和为2442.则六个数中最大的一个是 .
4.有一个四位数，在它的某位数字前加上一个小数点，再与这个四位数相加，得数是1997.7 8，这个四位数是___________.
5.有一类小于200的自然数，每一个数的各位数字之和是奇数，而且都是两个两位数的乘积 (例如144＝12×12).那么，这一类自然数中第三大的数是___________.
6.三个连续奇数的积的个位数最小是___________.
7.设A和B都是自然数，并且满足
，那么A+B＝___________.
8.一个六位数，十万位上的数是一个质数，万位上的数是一个合数，千位上的数是万位上 数的2倍，百位上的数是十万位与千位上的数的平均数，十位上的数是个位上数的3倍，已知 这个六位数的各位数字之和是9的倍数，那么这个数是___________.
9.甲乙两数的和是30，甲数的小数点向左移动一位后等于乙数的一半，那么甲数是 .
10.从1978到2010的自然数中，恰在拐弯处的数是 .
11.如图1，圆周上顺序排列着1，2，3，…，12这12个数，我们规定：相邻的四个数a1，a2，a3，a4，顺序颠倒为a4，a3，a2，a1称为一次“变换”(如1，2，3，4变 为4，3，2，1又如11，12，1，2变为2，1，12，11).能否经过有限次“变换”，将12个数 的顺序变为9，1，2，3，…8，10，11，12(如图2)?请说明理由.
第二节 数的整除
1.已知六位数□
□能被45整除，则所有满足条件的六位数共有
个.
2.如果六位数
能被85整除，那么它的最后两位数是
.
3.一个四位数能被两个连续的两位整数整除，这个四位数除以其中的一个，商是141；它除 以另一个，商比141大.这个四位数是 .
4.有四个数，每次选取其中三个数算出它们的平均数，再加上另外一个数，用这种方法计 算了四次，分别得到以下四个数：
86，92，100，106
那么，原来四个数的平均数是 .
5.某个七位数1993□□□能够同时被2，3，4，5，6，7，8，9整除，那么它的最后三位数 字依次是 .
6.修改五位数21847某一数位上的数字，可以得到737的倍数，那么修改后的数是 .
7.如果两数的和是64，两数的积可以整除4875，那么这两数的差等于 .
8.四个数的和是408，这四个数分别能被2、3、5、7整除，而且商相同.这四个数分别是 .
9.下面一个1983位数
□
中间漏写了一个数字(方框)，已知这个多位数能被7整除， 那么中间方框内的数字是
.
10.在29前面连续写上若干个1994，得到一个多位数…199429.如果这个多位数可 以被11整除，那么这个多位数的位数最少是 .
11.从1～9这九个数字中选出八个数字，分别组成能被12整除的、无重复数字的最小八位数 和最大八位数，则最小八位数是 ，最大八位数是 .
12.在2002后面补上三个数字，组成一个七位数，使它分别能被2、3、5、11整除，这个 七位数最小是___________.
13.从一个三位数中，减去7，则能被7整除；减去8，则能被8整除；减去9，则能被9整除. 这个三位数是 .
第三节 余数问题
1.1111+2×1111+3×1111+…+1111×1111被7除所得的余数是 .
2.在所有的两位数中，用较大的自然数除以较小的自然数，得到的余数最大可以达到 .
3.一个自然数被9除余1，所得的商被8除也余1.再把第2次所得的商除以8得商为a余7.又知 这个自然数被17除余4，所得的商被17除余15，商是a的2倍，这个自然数是 .
4.除以3余1，除以4，5，7不足2的三位数是 .
5.用某自然数a去除2002，得到的商是46，余数是r.则a= ，r= .
6.除以3余1，除以5余2，除以7余4的最小三位数是 .
7.两数相除商5余5，如果被除数扩大5倍，除数不变，则商是27，余数是3，原被除数是 ，除数是 .
8.7599除以一个质数，所得余数是9，这个质数最小是 .
9.678除以一个数，不完全商是13，并且除数与余数的差是8，除数是 ，余数是 .
10.一个三位数除以9余6，除以4余2，除以5余1，这样的数中最大的一个是 .
11.某三位数的各位数字都不为零，并且这个三位数被它的各位数字之和除，所得的商最小 可能是 .
12.8.77÷5.3除到一位小数时，商是1.6，余数是___________.
13.在下面算式的方框内填数，使带余数的除法的余数最大.
□÷78＝245…□
14.一个数能被3、5、7整除，若用11去除则余1.这个数最小是 .
15.某校五年级有学生若干人.
(1)若3人一行最后余2人，7人一行最后余2人，11人一行最后也余2人，五年级最少有学生多 少人?
(2)若3人一行最后余1人，7人一行最后余5人，11人一行最后余9人，五年级最少有学生多少 人?
第四节 约数与倍数
1.A＝2×5×7，B＝2×3×7，A和B的最大公约数是 ，最小公倍数是 .
2.三个连续整数的和是18，它们的最大公约数是 ，最小公倍数是 ___________.
3.三个质数的最大公约数是1，最小公倍数是105，这三个质数是 .
4.已知N为自然数，它是83的倍数，并且N2有63个因数，则N的最小值是 .
5.三个互不相等的自然数，已知每个数均为2的倍数，每两个数的和均为3的倍数，而三个 数的和为5的倍数，则这三个数的和最小是 .
6.9的约数有1，3，9三个，16的约数有1，2，4，8，16五个，那么144(即9×16)的约数共有 个.
7.三个互不相同的自然数之和为370，它们的最小公倍数最小能够是 .
8.有两个两位数的自然数，它们的最大公约数是8，最小公倍数是96，这两个自然数的和是 .
9.a,b,c是100以内的三个整数，a与b，a与c的最大公约数分别是12和15，a，b，c的最小公 倍数是120，那么，a，b，c分别是 .
10.把一张正方形的纸剪成边长是5厘米的小正方形，比剪成边长为6厘米的小正方形多99个 ，两种剪法都没有余下一点纸片，原来这张正方形纸的面积是 .
11.设n是一个四位数，它的9倍恰好是其反序数(例如：123的反序数是321).则n＝ .
12.恰有6个约数的两位数有 个.
13.把26、33、34、35、63、85、91、143分成若干组，要求每一组中任意两个数最大公约数是1，那么至少要分多少组?
14.庆祝“六一”节，学校扎了红花180朵，黄花234朵，白花360朵，把这些花扎成三色的花 束.所有的花束里的红花朵数相同，黄花朵数相同，白花朵数也相同，至多扎几束花正好把 花用完，每束中的红花、黄花、白花各几朵?
15.从运动场一端到另一端全长96米，从一端起到另一端每隔4米插一面小红旗.现在要改 成每隔6米插一面小红旗，问可以不必拔出来的小红旗有多少面?
16.一盒围棋子，4只4只数多3只，6只6只数多5只，15只15只数多14只，这盒围棋子在150- 200只之间.问这盒围棋子有多少只?
第五节 乘方与周期
1.1×1+2×1×2+3×1×2×3+4×1×2×3×4+5×1×2×3×4×5+6×1×2×3×4×5×6+7× 1×2×3×4×5×6×7+8×1×2×3×4×5×6×7×8＝___________.
2.20012001×20022002的末位数的数字是___________.
3.
×
积的尾数是___________.
4.1219-811的个位数是___________.
5.19491949的末位数是___________.
6.把8，88，888，……，
这1992个数相加，所得的个位数是 ，十位数是 ，百位数是 .
7.112＝121，1112＝12321
11112＝ 111112＝
问：(1)2＝ . (2)4321＝ 2
8.求
积的尾数.
9.1991个9与1990个8与1989个7的连乘积的个位数字是 .
10.先观察下面每一行的数有什么规律，然后在括号内填上一个适当的数，使它符合这个 规律.
(1)0，3，7，12， ，25，33，
(2)1，4，7，10， ，16，19
(3)2，6，18，54， ，486，1458
(4)1，4，9，16，25， ，49，64
(5)1，1，2，3，5，8， ，21，34，
(6)2，3，5，8，12，17， ，30，38
(7)1，4，13，40，121， ，
11.因为：
13＝1×1×1＝1
23＝2×2×2＝8
13+23＝1+8＝9
(1+2)2＝3×3＝9
13+23+33＝1+8+27＝36
(1+2+3)2＝6×6＝36
13+23+33+44＝1+8+27+64＝100
(1+2+3+4)2＝10×10＝100
……
那么：13+23+33+…+993+1003＝?
12.把自然数按下图规则从1开始排列：
第一行： 1
第二行： 2，3，4
第三行： 5，6，7，8，9
第四行： 10，11，12，13，14，15
……
在第100行中有 个数.
13.把你的猜想填入括号里.
(1)
9×6＝54
99×96＝9504
999×996＝995004
9999×9996＝
……
×
6＝
(2)
9×7＝63
99×97＝9603
999×997＝996003
9999×9997＝
……
×7＝
(3)若设9×k＝
(其中k=1，2，3，…，9，＝10A+B)，则猜想有 ：
×k＝
14.有数组：(1，1，1)，(2，4，8)，(3，9，27)，…，求第100组的三个数之和是多少?
15.四个小动物换位，开始小猪、小羊、小狗、小鹿分别坐在第1、2、3、4号位置上(如下图 ).第一次它们上、下两排换位，第二次左、右换位，第三次又上、下交换，第四次左、右 交换.这样交替进行下去，问十次换座位后，小狗坐在第几号座位上?
16.分析一下规律，再按照这个规律找出“?”所代表的数.
17.根据每小题前两组图形中三个数的关系，填出后一组图形空圈中的数.
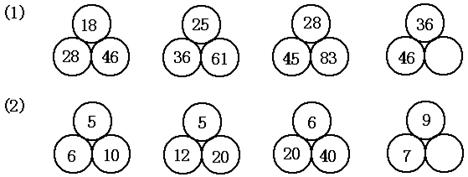
18.左下图是由九个小人排列的方阵，但有一个小人没有到位，请你从下面的6个小人中，选 一位小人放到问号位置，你认为最合适的人选是 号.
第六节 循环与近似
1.把
化成小数后将小数点后面的第1001位四舍五入，那么第1000位是
.
2.划去小数0.57383后面的若干个连续的数字后，再在最后一个数字上添上表示循环的小圆 点，得到的最大、最小的数分别是 .
3.假定n是一个自然数，d是1～9中的一个数码，若
＝0.d05，则n ＝
.
4.两个整数部分都是8的一位小数相乘，乘积用四舍五入法保留一位小数的近似值是68.1， 这两个数乘积的准确值是 .
5.在一个循环小数0.123456
中，如果要使这个循环小数第100位的数字是 5，那么表示循环节的另一个小圆点，应加在数字___________上.
6.在循环小数0.
B
中，已知小数点右边前1000位上各数 字之和为4664，且A，B，C中有两个数是相等的，则A，B，C分别是
.
7.在混合循环小数2.71828
的某一位上再添一个表示循环的圆点，使新产 生的循环小数尽可能大.请写出新的循环小数.
8.循环小数1.100102
，移动前一个循环的圆点，使新的循环小数 尽可能小，这个新的循环小数是___________.
9.循环小数0. 99251与0.
4563.这两个循环小数在小数点后第
位，首次同时出现该 位上的数字都是7.
10.分数
化成小数后，小数点后面第2001位上的数字是 .
11.0.7……(相邻的两个之间0的个数按自然数列顺序 递增)，这个无穷小数的小数点后的第1624位是多少?
12.两个带小数相乘，乘积四舍五入以后是60.0，这两个数都只是一位小数，两个数的整数 部分都是7.这两个带小数的乘积四舍五入以前是___________.
13.假定n是一个自然数，d是1～9中的一个数码，若
＝0.
d，则n=___________.
14.有一个小数为0.1213……998999，其中小数部分的数字由依次写下的整 数1～699得到的.问小数点右边第1995位数字是多少?
15.冬冬在计算乘法2.4乘以一个数a时，把2.4看成2.4 3，使乘积比正确结果减少0.5，则正确结果是( ).
16.已知
＝0.D
，其中A，B，C ，D是0～9中的不同数字，则A，B，C，D分别为_________.
17.把
化成小数后，小数点后第一百零一位的数字是( )，若
把小数点的一百个数字相加，所得的和是( ).
18.将
化为循环小数后，在小数点后面可找到一段数，使这段数的各 数字之和为2001.那么首次出现这一现象是从小数点后第 个数到第 个数.
19.0.
是纯循环小数，如果保留两位小数，取它的近似值是
.
第七节 分数问题
1.有甲、乙两个数，甲数的
等于乙数的
，甲数的
比乙数的
大45.甲数是 ，乙数是
.
2.两个分数之和等于1
，它们分子之比是5∶11，而分母之比是3 ∶7，这两个分数分别是
.
3.已知：A×120%＝×B＝C÷
＝D÷1
，把A，B，C，D四个数按从大到小的顺序排列起来.
4.有一个最简分数，把它的分子与分母都加上分母，所得到的新分数是原分数的3倍，这个 最简分数是 .
5.一个分数，如果分子加8，分母减10，它化简后的值等于；如果分子减3，分母减10，它化简后的值就等于，这个分数是
.
6.用
，
,1
分别去除某分数，所得的商都是整数，这个分数最小是
.
7.用
除或用
乘后的结果都是自然数的最小分数是
.
8.有一种最简分数，它们的分子与分母的乘积都是140，如果把所有这样的分数从小到大排 列，那么第三个分数是 .
9.一个分数，如果它的分子加上一个数，则等于，如果它的分母减 去同一个数，则等于
，原来这个分数是
.
10.1
，1，
，
，
，…是一串有规律的数，这串数中第9个数是 ，如果其中某个数的分母是1999，那么这个数的分子是___________.
11.一个最简分数，分子与分母的和是62，若分子减去1，分母减去7，所得新分数约简后为
，原分数是
.
12.有一个分数，分子比分母小13，若分子加上18，分母加上21，分数值不变，原分数是 .
第二章 计算问题
第一节 四则运算
1.3
×2345+5555÷
+654.3×36
2.
÷9÷3
3
÷
+8
4.2+0.039÷［×(2.31÷0.077)］-0.526
5.［0.314÷15.7+(5-3.47)×6
］÷104.2×
6.18÷2+0.65×
-×18+
×0.65
7.23.3×(2-75%)+56×1+(1+25%)×28.
8.
×
9.
×3.2+0.24÷
10.
+
×(3.625-3
)
11.1999×(5.22×1045+5
)÷(5.23×1045-5.22)
12.×(4.85÷-3.6+6.15×3)+［5.5-1.75×(1+
)］
13.［100×(+0.375)-2.25×］÷0.25
14.6.25×6.6+3.3×6+1.1×625%
15.24×(4
-2)-0÷1÷0.314
第二节 简便算法
1.9998+998+99+9+6
2.
3.
4.3
5.
6.1-(
)-(
)-(
)-(
)
7.×÷÷
8.×444711+×136481
9.
10.
11.1998×(
)+11×(
)-2009×(
)+3
12.(20
×1.65-20
×20)×47.5×0.8×2.5+10÷5
13.4÷1+0.31×0.6+0.19×
14.2
×3
×5÷(3.35 ×5.625×2.12)
15.
16.56789×99999
17.
18.×1235-×1234
19.3
+46
×0.25+0.625×46+46×0.125
20.(3.14×7.42+2.58×3.14)÷(3.25+3.14-3)
21.
×511
22.(9.79×4
+3×4
)×( 3-1÷
)
23.1-
24.(3.91+3+6.09+6)×(2-1.125)+(1÷-1.5)×6
25.9+99+999+9999+1
26.9999×2222+3333×3334
27.
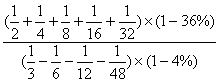
28.1993×199.2-1992×199.1
第三节 分数的拆分
1.在下列等式的括号里填适当的数.(分母不能重复)
(1)
＝
(2)
＝
+++
(3)
＝++ (4)= ++++
2.计算题：
(1)94×56.87+94×43.48+6×100.35
(2)8--
(3)4
(4)(12-
×2)+(10-×8)+(8-×4)+(6-×12)+(2-×6)+(4-×10)
(5)
+
+
+…+
+
(6)
+
+
+
+
+
(7)(1-)×(1-)×(1-) ×(1-
)×(1-
)×(1-
)×(1-
)
(8)
(9)
(10)
(11)1992+-1+2-3+4-5+…+1990-1991
(12)( -)+(-)+(-)+…+(
-
)
(13)(1+
)+(1+×2)+(1+×3)+…+(1+×10)+(1+×11)
(14)
(15)1×1×1×1×…×1
(16)
+
+…+
(17)1+2+3+4+…+20
(18)(1+
)+(1+×2)+(1+×3)+…+(1+×10)+(1+×11)
(19)(1-
)×(1-
)×…×(1-
)
(20)1
(21)(4
×4.8+4
×5
)÷5
÷2
第四节 其他简算方法
计算题
1.1+2+3+…+1989+1990
2.(1+3+5+…+1989)-(2+4+6+…+1988)
3.1992-1988+1984-1980+1976-1972+……+8-4
4.1-3+5-7+9-11+…-1999+2001
5.1.725+2.725+3.725+…+60.725
6.(2
)×(4-
)
7.40556+8074+9444+926+11000
8.(
+…+
)＋(+
+…+
)+(++
+…+
)+…+(
+
)+
9.
10.302-292+28+-272+…+42-32+22+12
11.1+
+
+
+ …+
12.(
)2+()×-(1++++++
)×(
)
13.1+2
14.
×+
15.
+…+
16.1+2-3-4+5+6-7-8+9+10-11-12+…+1982-1983-1984+1985+1986-1987-1988+1989+1990
17.1992+1991-1990-1989+1988+1987-1986-1985+…+4+3-2-1
18.1992-1989+1986-1983+…+12-9+6-3
19.10×
＝
＝?
第五节 繁分数化简
化简
1.
2.49÷2
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.