综合能力训练
一、填空题。
1.把下面的“成数”改写成百分数。
五成( )、七成( )、三成五( )、十成( )
2.把下面的百分数改写成“成数”
30%( ) 45%( ) 10%( ) 95%( )
3.利息=( )×( )×( )
4.30千克是50千克的(%),50千克是30千克的( %)
5.5吨比8吨少(%),8吨比5吨多(%)。
6.540米是( )米的20%。
7.( )公顷的25%是20公顷。
![]()
二、判断题。(对的画“√”,错的画“×”)
1.利息和本金的比率叫利率。 ( )
2.一块地的产量,今年比去年增长二成五,就是增长十分之二点五。 ( )
3.一种药水,水和药的比是1∶20,水占药水的5%。 ( )
![]() ( )
( )
三、选择题。(把正确答案的序号填在括号里)
1.半成改写成百分数是 ( )
A.50%
B.0.5%
C.5%
2.一块地原产小麦25吨,去年因水灾减产二成,今年又增产二成。这样今年产量和原产量比 ( )
A.增加了
B.减少了
C.没变
3.小英把 1000元按年利率2.45%存入银行。两年后计算她应得到的本金和利息,列式应是 ( )
A.1000×2.45%×2
B.(1000×2.45%+1000)×2
C.1000×2.45%×2+1000
四、计算题。

![]()
![]()
五、应用题。
1.一块小麦实验田,去年产小麦24.5吨,今年增产了二成。这块实验田今年产小麦多少吨?
2.一块地,去年产水稻12吨,因水灾比前年减少二成五。这块地前年产水稻多少吨?
3.李英把5000元人民币存入银行,定期1年,年利率是2.25%。到期时,李英应得利息多少元?
4.王钢把10000元人民币存入银行,定期3年,年利率是2.7%。到期时,王钢应得本金和利息一共多少元?
5.一块棉花地,去年收皮棉30吨,比前年增产了5吨。这块棉花地皮棉产量增长了几成?
6.一个养殖场,养鸭的只数比养鸡的只数少20%,养的鸡比鸭多1000只。这个养殖场养鸭多少只?
![]()
相遇。甲车每小时的速度是85千米,乙车的速度是甲车的120%。A、B两地相距多少千米?
*8.张晶在银行存了30000元人民币,定期五年,年利率是2.88%。到期时交纳利息所得税20%后,银行应付给张晶本金和利息一共多少元?(选作)
参考答案
一、
1.50% 70% 35% 100%
2.三成四成五一成九成五
3.本金×利率×时间
4.60% 167%
5.37.5% 60%
6.2700
7.80
8.4 20 40%
二、1.√ 2.√ 3.× 4.×
三、1.C 2.B 3.C
![]()
五、
1.24.5×(1+20%)=29.4(吨)
2.12÷(1-25%)=16(吨)
3.5000×2.25%=112.5(元)
4.10000×2.7%×3+10000=10810(元)
5.5÷(30-5)=20%,增长2成。
6.1000÷20%×(1-20%)=4000(只)
或1000÷20%-1000=4000(只)
![]()
8.30000×2.88%×5×(1-20%)+30000=33456(元)
综合能力训练
一、填写( )的内容。
1.表示两个比相等的式子叫做( )。
2.0.32∶1.6化成最简单的整数比是( ),比值是( ),根据这个比值组成一个比例式另一个比是( ),比例式是( )。
![]()
10和60,这个比例是( )。
4.被减数是72,减数和差的比是4∶5,减数是( )
5.因为a×b=c,当a一定时,b和c( )比例。
当b一定时,a和c( )比例。
当c一定时,a和b( )比例。
6.用20的约数组成一个比例式是( )。
![]()
一个外项是( ),这个比例式是( )。
![]()
应画( )厘米。
9.在绘画时,要把实际距离缩小500倍,使用的比例尺应该是( )。
二、分析判断。(对的画“√”,错的画“×”)
1.一般地图上用的比例尺是缩小比例尺。 ( )
2.圆的直径和它的面积成正比例。 ( )
3.y=5x,x和y成反比例。 ( )
4.数a与数b的比是5∶8,数a是75,数b是120。 ( )
![]() ( )
( )
三、分析选择。将正确答案的序号填在( )里。
1.甲乙两个圆半径的比是2∶1,那么甲和乙两个圆的面积的比是 ( )
(1)4∶1
(2)2∶1
(3)4∶2
2.把一个圆柱体加工成一个与它等底等高的圆锥体,圆柱的体积与去掉部分的体积的比是 ( )
(1)3∶1
(2)3∶2
(3)2∶3
3.在一个比例式中,两个比的比值都等于3,这个比例式可以是 ( )
(1)3∶1=1∶3
(2)3∶1=0.3∶0.1
(3)9∶3=3∶1
4.修一条路,已修的是未修的80%,已修的与未修的比是 ? ( )
(1)80∶100
(2) 4∶5
(3)10∶8
![]() 刘师傅现在与过去工作效率的比是 ( )
刘师傅现在与过去工作效率的比是 ( )
![]()
(2) 1∶3
(3) 3∶1
四、观察分析。
1.将下面的等式改写成比例式。
(1) 10.2×9=1.8×51
![]()
(3)51×7=17×21
(4)62a=47b
2.认真观察下面每题的解是否正确?对的画“√”,错的改正过来。
(1)15.6∶2.8=2.4∶x
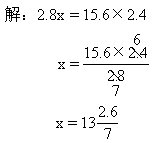
![]()
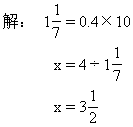
![]()

![]()
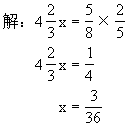
五、说说下面各题的两种相关联的量是成正比例,还是成反比例。写出说理过程。
1.小麦的重量一定,面粉和出粉率。
2.图上距离一定,比例尺和实际距离。
3.先判断,再填空。
3a=b a和b成( )比例。

六、选择正确算式,并说出理由。
1.一辆汽车从甲地开往乙地,每小时行驶28千米,4.5小时到达,要4小时到达,每小时要多行几千米?
(1)28×4.5÷4-28
(2)解:设每小时多行x千米。
28×4.5=(28+x)×4
(3)解:设每小时多行x千米。
28×4.5=28×4+x
(4)28-28×4.5÷4
2.东风洗染厂,每天用水量比过去节约20%,原有390吨水,现在比过去多用30天,现在每天用水多少吨?
(1)390×(1-20%)÷30
(2)解:设现在每天用水x吨。
390×20%=30x
(3)解:设过去用x天,则现在用(x+30)天。

390÷(120+30)=2.6(吨)
(4) 390×20%÷30
七、解决下面的实际问题。
1.一幅地图用0.6厘米表示实际距离30千米,求这幅地图的比例尺。用线段比例尺表示出来。
2.张庄和王村相距960千米,要在两村间修筑一条笔直的马路,画在设计图上的距离是
![]()
这幅设计图的比例尺是多少?
![]()
这样可以提前几天完成?(用三种你认为简捷的方法解答)
4.一块平行四边形菜地,底与高的和是150米,它们的比是3∶2,求这块菜地的面积是多少平方米?
*5.甲乙两地相距800千米,A、B两辆汽车分别从两地同时相向而行,已知A、B两车速度比是6∶5,当两车相遇时,两车各行多少千米?(用三种方法解答)
参考答案
一、
1.比例
![]()
3.10∶30=20∶60
4.32
5.正正反
二、1.√ 2.× 3.× 4.√ 5.√
三、1.(1) 2.(2) 3.(2) (3) 4.(2) 5.(3)

2.(1)× (2)√ (3)√ (4)×
五、1.正比例 2.反比例 3.正(表略)
六、
1.(1) (2)
2.(2) (3) (4)
七、
1.
![]()
2.1∶
3.方法1 30-8÷5=10(天)
![]()
方法3 解:设实际x天完成。(把一份稿件看为“1”)
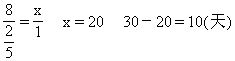
![]()

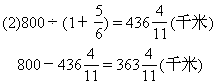
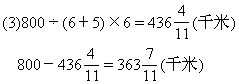
综合能力训练
一、将正确答案填在( )里。
1.从圆锥的( )到( )的距离是圆锥的高,圆锥有( )条高。
2.圆柱的体积是( )的圆锥体积的3倍,所以圆锥体积的公式是( )。
3.把4个同样大小的圆柱,熔铸成等底等高的圆锥,能熔铸( )个。
4.一个圆柱的体积是60立方厘米,和它等底等高的圆锥的体积是( )。
5.把一段圆柱形圆木,加工成等底等高的圆锥体,削去部分体积是圆柱体积的( ),是圆锥的( )。
6.用一张长是25.12厘米,宽3.14厘米的长方形厚纸板围成直圆柱,有( )种围法;其中一种围成的圆柱的高是( )厘米,直径是( )厘米;另一种围的圆柱的高是( )厘米,直径是( )厘米。
二、观察思考下面的解题过程和结果,是否正确?
1.一根圆柱形水管,内直径20厘米,水流的速度是每秒4米,这个水管1分钟可以流过多少立方米的水?
解:(1)圆柱形水管的底面积
![]()
(2)圆柱形水管的容积(4米相当圆柱的高)
314×400=125600(立方厘米)
(3)1分钟可以流过多少水
125600×60=(立方厘米)
立方厘米=7.536立方米
答:这个水管1分钟可以流过7.536立方米水。
2.有一根长20厘米,半径为2厘米的圆钢,在它的两端各钻了一个深为4厘米,底面半径为2厘米的圆锥形小孔做成一个零件,如图这个零件的体积是多少立方厘米?
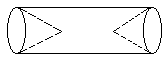
解:(1)圆柱的底面积
2×2×3.14=12.56(平方厘米)
(2)圆柱的体积
12.56×20=251.2(立方厘米)
(3)圆锥形小孔的体积
12.56×4=50.24(立方厘米)
(4)零件的体积
251.2-50.24=200.96(立方厘米)
答:这个零件的体积是200.96立方厘米。
3.一个高3分米,底面直径为20厘米的圆柱形水桶里装满水,水中放着一个底面直径为18厘米,高为15厘米的铁质圆锥体,当这个铁质圆锥体取出后,会发生怎样的变化?结果如何?
解:当这个铁质圆锥体取出后,桶内水面要降低,因为这个物体原来占据了一些空间,结果怎样,就要先求圆锥体的体积,再求变化的结果。
(1)圆锥的底面积
![]()
(2)圆柱的底面积
![]()
(3)圆锥的体积
![]()
(4)水面降低的米数
1271.7÷314=4.05(厘米)
三、综合运用知识解决实际问题。
1.有A、B两个容器,如图,先把A容器装满水,然后将水倒入B容器,B容器中水的深度是多少厘米?
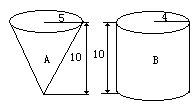
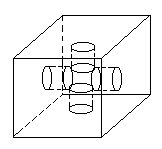
*2.如右图,是一个棱长为4分米的正方体零件,它的上、下、左、右面上各有一个半径为2厘米的圆孔,孔深为1分米,这个零件的表面积是多少?体积是多少?
*3.把一个直径是2分米的圆柱的底面分成许多相等的扇形,然后沿直径把圆切开,拼成一个和它体积相等的长方体,这个长方体表面积比原来圆柱的表面积增加8平方分米,这个长方体的体积是多少?
*4.如图,这顶帽子,帽顶部分是圆柱形,用花布做的,帽沿部分是一个圆环,也是用同样花布做,已知帽顶的半径,高和帽沿宽都是1分米,那么做这顶帽子至少要用多少平方分米的花布?

*5.把一个长7厘米,宽6厘米,高4.5厘米的长方体铁块和一个棱长5厘米的正方体的铁块,熔铸成一个大圆柱体,这个圆柱体的底面积是78.5平方厘米,那圆柱的高应是多少厘米?
参考答案
一、
1.顶点 底面圆心 1。
![]()
3.12
4.20立方厘米
![]()
6.2,25.12厘米,1厘米,3.14厘米,8厘米
二、1.正确 2.错误 3.正确
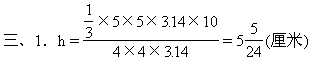
2.提示:正方体零件的表面积增加了4个小圆柱的侧面积。正方体零件的体积减少了4个小圆柱的体积。
表面积:4×4×6×100+3.14×2×2×10×4=10102.4(平方厘米)
体积:4×4×4×1000-2×2×3.14×10×4=63497.6(立方厘米)
3.提示:表面积增加8平方分米,实际是两个以半径为宽,高为长的长方形。
8÷2÷(2÷2)=4(分米)高
3.14×(2÷2)2×4=12.56(立方厘米)或
8÷2×3.14×2÷2=12.56(立方厘米)
4.18.84平方分米
5.4厘米
综合能力训练
一、看表填空。
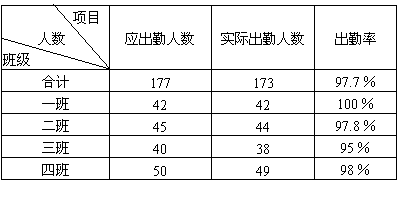
1.建华小学六年级学生参加植树活动各班出勤情况如下:
一班:应到42人,实到42人。
二班:应到45人,实到44人。
三班:应到40人,实到38人。
四班:应到50人,实到49人。
完成下面的统计表。

2.在( )中填上适当的数。
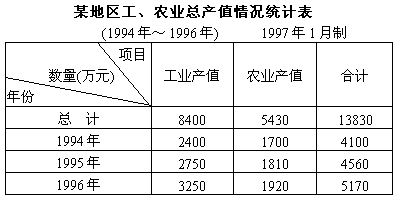
(1)1994年~1996年某地区三年内工业总产值占工农业总产值的( )%
(2)1995年的农业总产值占当年工农业总产值的( )%。
(3)1996年的工业产值比1994年工业产值增长( )万元。
(4)1996年的工农业总产值比1995年工农业总产值增长( )%
二、看图填空。
1.

(1)( )月份的产量最高,是( )吨。
(2)( )月份的产量最低,是( )吨。
(3)下半年的月平均产量是( )吨。
(4)这是( )统计图。
(5)9月份的产量比八月份的产量增长了( )%
2.
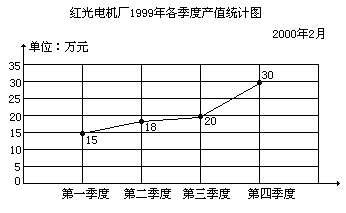
(1)这是( )统计图,它不但可以表示( )的多少,而且能够清楚地表示数量( )的情况。
(2)第( )季度产值最高,它比第三季度增产( )%。(3)全年总产值是( )万元
(4)下半年完成总产值的( )%。
(5)下半年比上半年产值增加了( )%。
三、看图列式解答。

(1)下半年平均每月产糖( )吨(保留整数)。
(2)第四季度比第三季度增产( )%。
(3)8月份的产量比7月份增产( )%。
(4)12月份的产量占下半年产量的( )%。
(5)第三季度的产量占下半年产量的( )%。
(6)10月份的产量占下半年产量的( )%。
参考答案
一、1.
2.(1)60.7 (2)39.7 (3)850 (4)13.4
二、1.(1)12、26 (2)7、12 (3)20 (4)条形 (5)11.8
2.(1)折线数量增减变化 (2)第四季度 50 (3)83
(4)60.2 (5)51.5
三、(1)262 (2)70.7 (3)33.3 (4)23.6 (5)36.9 (6)19.1
综合能力训练
一、填空。
1.4.12小时=( )分
![]()
![]()
( )个这样的分数单位就是最小的质数。
3.十一亿六千零二十万,写作( ),把它改写成用亿作单位的数是( )。
4.圆周率一定,圆的周长和它的直径成________比例。
![]()
6.18的约数有( ),选出其中的四个数组成一个比例,比例是( )。
![]()
8.有一个小数,先将它的小数点向左移动两位后,再扩大1000倍得40.3,原来的小数是( )。
9.一个圆锥体的体积是40立方厘米,比与它等底的圆柱体小20立方厘米,如果圆锥高10厘米,圆柱的高是( )厘米。
![]()
来它的分子分母的和是28,这个分数是( )。
二、选择正确答案填在( )里。
1.a·a可以写作 ( )
①2a
②a2
③a+a
![]()
用42分钟,乙行这段路用________分钟。 ( )
①30
②36
③49
![]() ( )
( )
①2∶3
②3∶4
③3∶2
4.7是21和42的 ( )
①质因数
②公约数
③最大公约数
![]()
两堆煤的重量比是 ( )
①5∶3
②4∶5
③2∶5
三、判断。(对的画“√”,错的画“×”)
1.一个圆的半径是3厘米,它的周长和面积相等。 ( )
![]() ( )
( )
3.去掉小数点后面的“0”,小数的大小不变。 ( )
4.12不能被8整除,但能被8除尽。 ( )
5.真分数都是最简分数。 ( )
![]() ( )
( )
7.六年级同学参加植树劳动,出勤100人,缺勤3人,缺勤率是3%。 ( )
8.一幅地图,图上距离5厘米表示实际距离5千米,这幅地图的比例尺是1∶100000。 ( )
四、求未知数x。
![]()
五、计算下面各题,能简算的要简算。
1.19175÷59+678
2.36.5×1.4-8.51÷3.7
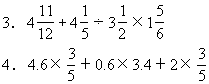
![]()
六、按要求列式计算。

七、选择正确的算式填在( )里。
1.生产一批零件,前3天生产124个,照这样计算,需再用12天完成全部任务。这批零件共有多少个?如果设这批零件共x个。正确的算式是 ( )
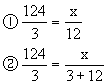
③12x=124×3
2.菜市场有黄瓜150千克,黄瓜重量和西红柿重量的比是3∶5,黄瓜重量比西红柿少多少千克?正确的算式是 ( )
①150÷3×5
②150÷3×5-150
③150÷3×(5-3)
![]()
八、应用题。
1.一桶油,用去20%,还剩32千克,这桶油原有多少千克?
2.一堆煤,原计划每天烧450吨,10天烧完。实际只用9天就烧完了,每天烧多少吨?(用算术和比例两种方法解)
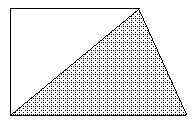
3.量出计算阴影面积所需数据(量得结果取整厘米数并写在图上),再计算出阴影部分面积。
4.下面是五(4)班一次数学测验情况统计图,请看图回答问题。回答后再试着提出几个问题,请同伴回答。

(1)达到良以上的共( )人,占全班人数的( )%。
(2)优秀的有( )人,占全班人数的( )%。
(3)达标的有( )人,占全班人数的( )%。
![]()
合唱队调出6人到田径队,则合唱队与田径队人数的比是3∶4,合唱队原有多少人?
6.两辆汽车分别从AB两地同时出发,在距中点40千米处相遇,甲行全程需10小时,乙行全程需15小时。求AB两地距离。(用多种方法解答)
参考答案
一、
1.247.2 1 6250
![]()
3. 11.602亿
4.正
5.2∶3
6.1 2 3 6 9 18 3∶9=2∶6
![]()
8.4.03
二、1.a2 2.49 3.3∶2 4.公约数 5.5∶3
三、1.× 2.√ 3.× 4.√ 5.×6.×7.×8.√
四、1.x=2 2.x=1
![]()
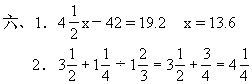
![]()
![]()
八、
1.32÷(1-20%)=32÷80%=40(千克)
2.450×10÷9=500(吨)
解:设每天烧x吨。
450×10=9x
x=500
3.解:底6厘米,高3厘米
6×3÷2=9(平方厘米)
4.40 80 5 10 10 20

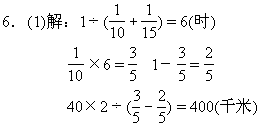
(2)解:10∶15=2∶3
40×2÷(3-2)×(3+2)=400(千米)