說明:本試卷共計30題填充題,滿分150分。請依題號將答案填入答案卷中。
甲. 1~10題每題4分
01.
請計算![]() 之值。
之值。
ANS: 61700 (2468×100÷4=246800÷4=61700)
02. 請計算1.997 + 19.99 + 200.1 + 2003之值。
ANS: 2225.087
03.
今有甲、乙、丙三個正數, 已知甲數的![]() 等於乙數的
等於乙數的![]() , 乙數的
, 乙數的![]() 等於丙數的
等於丙數的![]() . 請問哪一個數最小 ?
. 請問哪一個數最小 ?
ANS: 丙 (甲:乙:丙 = 225 : 200 : 192)
04. 有一群羊, 五五數之餘一, 七七數之餘三, 九九數之餘五. 若已知此群羊約有六百多隻, 請問此群羊的確實數量有幾隻 ?
ANS:626隻 (n+4=5,7,9之公倍數)
05. 如下圖所示, 請計算圖形中陰影部份之面積 (長度單位為公分) 。
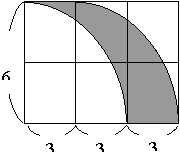
ANS: 18 cm2 (6×9–6×6=18或移補 2×3×(6÷2)=18)
06. 下表中, 同行之上下兩符號組成一對新編碼, 如第1組編碼為 Ch, 第2組編碼為Di, 請問第23組編碼是什麼 ?
| C | D | E | C | D | E | C | D | E | ---- |
| h | i | j | k | h | i | j | k | h | ---- |
ANS: DJ (23![]() 2(mod3);23
2(mod3);23![]() 3(mod4))
3(mod4))
 07. 現有6個數, 它們的平均數是 25, 前 3個數的平均數是 21, 後 4個數的平均數是 32. 請計算第3個數之值。ANS: 41 (3×21+4×32–6×25=41)
07. 現有6個數, 它們的平均數是 25, 前 3個數的平均數是 21, 後 4個數的平均數是 32. 請計算第3個數之值。ANS: 41 (3×21+4×32–6×25=41)
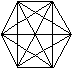
08. 如右圖是一個邊長 1 公分的正六邊形. 請問圖中菱形共有幾個?
ANS: 9個 (一個正六邊形頂點, 可畫出一個菱形,計6個菱形;內部可
畫出3個較大菱形,合計9個菱形)
 09. 如圖所示, 用繩子把兩個半徑為 10 cm的圓筒捆綁在一起, 如果接頭處用了15 cm 的繩子, 請問完成這項工作需用多長的繩子 ? (圓周率
09. 如圖所示, 用繩子把兩個半徑為 10 cm的圓筒捆綁在一起, 如果接頭處用了15 cm 的繩子, 請問完成這項工作需用多長的繩子 ? (圓周率![]() 取 3.14)
取 3.14)
ANS: 117.8 cm (2×3.14×10+2×(10+10)+15=117.8)
10. 在A, B, C, D, E中分別填入適當數字可以完成下述三句常用成語:
(I). 推A阻B; (II). C勞永逸; (III). D年E載
並使 AB + C = DE此一數字算式成立. 請計算
![]() 之值?
之值?
ANS: 25 (2×A–B+C–D+5×E=2×3–4+1–3+5×5=25)
乙. 11~20題每題5分
 11. 有棋盤式街道如下圖. 街道均為單行道(只能往下走或往右走), 今小明欲從甲點走到丙點, 途中需經乙點, 請問小明共有幾種走的路徑可以選擇 ?
11. 有棋盤式街道如下圖. 街道均為單行道(只能往下走或往右走), 今小明欲從甲點走到丙點, 途中需經乙點, 請問小明共有幾種走的路徑可以選擇 ?
| 乙 | |||||
|
|
ANS: 30種走法 (5×6=30)
12. 設有一凸多邊形, 其內角度數分別為最大172度, 其餘為168度、164度、160度 ……. 請問此多邊形的邊數為多少 ?
ANS:12邊形 (![]() )
)
13. 你只有兩個瓶子, 它的容量分別是18公升和14公升. 若水能無限制供應, 請問你可以量得下列那種水量 ?
(A) 5公升 (B) 7公升 (C) 8公升 (D) 9公升 。
ANS:C (18x+14y=c![]() )
)
14.
如果一分數![]() 中, 分子與分母同時相等正量增加, 請問此分數
中, 分子與分母同時相等正量增加, 請問此分數![]() 之值有何變化 ?
之值有何變化 ?
(A) 其值會變小 (B) 其值會變大 (C) 其值保持不變
(D) 沒有足夠資訊可以判斷其值如何變化 。
ANS:B (因為等正量增加,所以其值變大)
15. 請問:時間在九點半時, 分針和時針所成的角是幾度 ?
ANS:105度(時針於九點半時, 又往12點方向走了![]() )
)
16. 如果今日是星期五, 請問再過![]() 天, 是星期幾 ?
天, 是星期幾 ?
ANS: 星期六 (![]() )
)
17. 把一條細繩對折三次後 (即對折, 對折再對折), 再從中間剪開,請問剪開後
的細繩共分成幾段 ?
ANS: 9段 (![]() )
)
18. 如果甲, 乙, 丙三個小於10的非負整數滿足下述加法關係
 ,
,
請問 ![]() 之值為何 ?
之值為何 ?
ANS: 21 (![]() )
)
 19. 圖中ABCD是一個等腰梯形,其中
19. 圖中ABCD是一個等腰梯形,其中![]() 平行於
平行於![]() ,且
,且![]() =
=![]() 。
。
如果![]() =20cm,∠ACB=30o,求等腰梯形ABCD的面積。
=20cm,∠ACB=30o,求等腰梯形ABCD的面積。
ANS: ![]() (
(![]() …由 A向底作垂足, 移補成長方形)
…由 A向底作垂足, 移補成長方形)
20. 請問: 整除990000且自身為 3 的倍數但不被125整除之正整數有幾個 ?
ANS: 60個 (![]()
![]() )
)
丙. 21~30題每題6分
21. 請問: 介於1001與2003的整數中, 有多少個整數恰有三個相同的數字 ?
ANS: 36 個 (1011, 1211, …, 1911; 1101, 1121, …, 1191; 1110, 1112, …, 1119…個 1,共計27個; 1222, …, 1999, 2000…3個2, …, 9, 0,共計9個,合計36個)
22. 餐廳裡有花生, 巧克力, 芋頭, 薄荷口味的四大桶冰淇淋供客人隨意取用.
現在阿宏帶著大, 小兩丸子前去取用冰淇淋, 三人皆取用一杯冰淇淋, 請問
阿宏父女三人有多少種取用冰淇淋的選擇 ?
 ANS: 64 種 (43=64)
ANS: 64 種 (43=64)
23. 如圖所示, 請問圖形中共有梯形幾個 ?
ANS: 60 個 (橫向(3+2+1)×縱向(4+3+2+1)=60)
24. 下圖所示, 2點可決定1條直線, 三點最多可決定3條直線, 四點最多可決定6條直線, 五點最多可決定10條直線. 請問14個點最多可決定幾條直線 ?
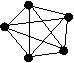 | |||||||
ANS:91 條(![]() )
)
25. 現定義新運算![]() 如下所述:
如下所述:
![]() , 其中
, 其中![]() 與
與![]() 為我們平常所使用之乘法與加法運算. 請計算
為我們平常所使用之乘法與加法運算. 請計算![]() 之值。
之值。
ANS:1(![]() )
)
26. 請計算符合下述關係之甲值。
| 35 | 21 | 19 | 46 | 28 | 34 | 43 | 52 | |||
| 245 | 479 | 368 | 甲 |
ANS: 563或493 (52 ; 43 + 52 ; 43 )、(52-43+40)3
 27. 若己知長方形 ABCD之長 AD為 6 cm, 寬 AB為 3.5 cm, CDEF為一平行四邊形, 三角形 BEH的一邊 BH為 2 cm. 請問下圖中之陰影面積為何 ?
27. 若己知長方形 ABCD之長 AD為 6 cm, 寬 AB為 3.5 cm, CDEF為一平行四邊形, 三角形 BEH的一邊 BH為 2 cm. 請問下圖中之陰影面積為何 ?
ANS: 14 cm2 (![]() )
)
28. 現在甲, 乙兩人在長為 60 公尺的游泳池之相對兩端同時出發, 游到另一端便立即返回. 若甲每秒游 3公尺而乙每秒游4公尺. 請問從出發開始計時5分鐘內, 甲, 乙兩人相遇幾次 ?
ANS: 18次
![]()
29. 某日, 小明, 小華與小新三個調皮的學生, 打算跟老王開個小玩笑, 三人協議各自說三句話, 其中恰有一句話, 故意說錯, 請老王判斷真相究竟為何 ?
小明:我拿了 22 元, 比小華少拿 2 元, 但比小新多拿 1元。
小華:我拿的錢不是最少的,小新拿的錢跟我拿的差 3 元, 小新拿了 25 元。
小新:我拿的錢比小明拿的少, 小明拿了 23 元, 小華比小明多拿 3 元。
請問: 小明, 小華與小新共拿了多少元 ?
ANS: 70元 (小明 23元, 小華 25元, 小新 22元 …小明: 我拿了 22 元; 小新:小明拿了 23 元 …必有一句是真話 !!! )
30.
下圖所示之立體, 是將一個長 30 cm, 寬 20 cm, 高 15 cm 的長方體, 在其上面正中央挖去半徑為 3 cm 的半圓柱, 並在其右側邊緣挖去半徑為 2 cm 的四分之一圓柱. 請問此立體之體積為多少立方公分 ? (圓周率![]() 取 3.14)
取 3.14)
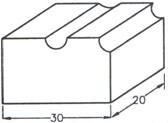
ANS: 8654.6 cm3 (30×20×15–![]() ×3.14×32×20–
×3.14×32×20–![]() ×3.14×22×20=8654.6)
×3.14×22×20=8654.6)